correction DS PIII, PIV, CIV

1S DEVOIR SURVEILLE CIV et PIII et PIV
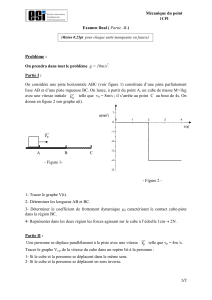
EX I : Forces
Données : Intensité de la pesanteur : g = 9,81 N.kg-1
Masse volumique de l’eau : ρeau = 1,00.103 kg.m-3
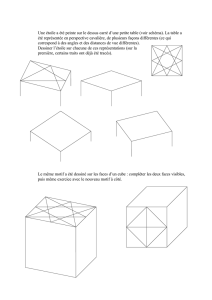
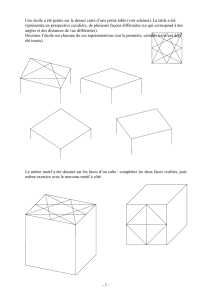
1) Un cube, de masse m = 115 g, est suspendu à l’extrémité d’un ressort de raideur k.
Lorsque le cube est en équilibre, le ressort est allongé de ΔL = x = 4,50.10-2 m. Voir schéma :
a) Faire le bilan des forces appliquées au cube. On négligera la poussée d’Archimède exercée par l’air.
Sachant que le cube est pseudo-isolé, écrire la relation vectorielle reliant ces forces.
b) Calculer le poids P du cube et représenter les forces appliquées au cube sur le schéma ci-contre avec 1 cm pour 1 N.
c) Déterminer la valeur de la constante de raideur du ressort k en fonction de m,g et x
2) Le cube est ensuite immergé entièrement dans l’eau. A l’équilibre, la tension exercée par le ressort est alors T = 1,01 N.
On note Pa la valeur de la poussée d’Archimède exercée par l’eau. On admet que T + Pa - P = 0 N.
En déduire la valeur de Pa et calculer le volume V du cube.
EX II : Lois de Newton
On étudie le mouvement d’un cube de centre de gravité G et dont le poids est P = 0,20 N (voir annexe).
Dans les trois phases du mouvement, les actions mécaniques de l’air sont négligeables.
Donnée : intensité de pesanteur g = 9,8 N.kg-1
PHASE 1 : le cube est en équilibre sur une table horizontale.
Le cube est soumis à l’attraction terrestre F Terre/Cube et à la réaction de la table F Table/Cube .
1) Pourquoi F Terre/Cube = - F Table/Cube ?
2) Montrer que F Terre/Cube = F Cube/Table . Quelle loi de Newton utilisez-vous ?
PHASE 2 : le cube glisse sur un plan incliné, en ligne droite, à vitesse constante.
Le cube est toujours soumis à son poids P à la réaction R du plan incliné.
1) Le cube est-il pseudo-isolé ? Justifier précisément la réponse.
2) Représenter le vecteur poids du cube sur l’annexe avec 1 cm pour 0,04 N.
Construire ensuite les deux composantes Rn et Rt de la réaction du plan incliné.
3) Déterminer graphiquement l’intensité de la force de frottement exercée par le plan incliné sur le cube.
PHASE 3 : le cube chute dans le vide.
1) Calculer la valeur de la vitesse du centre de gravité du cube aux points G4 et G6.
2) Représenter les vecteurs vitesse vG4 et vG6 avec l’échelle 1 cm pour 0,05 m.s-1.
3) Construire le vecteur ΔvG5 = vG6 - vG4 , variation du vecteur vitesse du centre de gravité au point G5.

4) Représenter le poids du cube au point G5 et comparer avec ΔvG5 . Commenter.
EX III : Conductance et conductivité
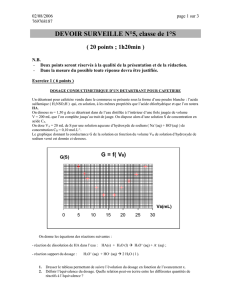
On veut mesurer la conductivité d’une solution de chlorure de sodium. On utilise une cellule constituée de 2 plaques
métalliques parallèles de surface S = 40 cm2, séparées d’une distance L = 1,0 cm. L’expérience montre que pour une tension
de 6,0 V, l’intensité du courant qui traverse la solution est 240 mA.
1) De quoi dépend la conductance d’une solution ?
2) Calculer la conductance G de la solution.
3) Calculer la constante de cellule kcell = S ÷ L. En déduire la valeur de la conductivité σ de la solution en S.m-1.
EX IV : Conductivité d’un mélange de solutions
Données : Conductivités molaires ioniques en S.m2.mol-1 : K+ = 73,5. 10-4 ; Na+ = 50,1.10-4 ; HO- = 198,6. 10-4
1) On prépare V1 = 10,0 mL d’une solution aqueuse S1 d’hydroxyde de potassium (KOH K+ + HO-) de concentration molaire
en soluté apporté C1 = 5,00.10-3 mol.L-1.
a) Montrer que la concentration molaire effective des ions K+ est [K+] = C1. On admettra que [HO-] = C1.
b) Calculer σ1 la conductivité de la solution S1.
2) On prépare V2 mL d’une solution S2 d’hydroxyde de sodium (NaOH Na+ + HO-) de concentration C2.
On admet que les concentrations molaires effectives des ions sont [Na+] = [HO-] = C2.
Exprimer, sans faire de calcul, σ2 la conductivité de la solution S2, en fonction de C2, Na+ et HO-.
3) On mélange S1 et S2. On admet que [K+] = C1  V1  ( V1 + V2 ) et [Na+] = C2  V2  ( V1 + V2 )
a) Montrer que [HO-] = (C1  V1 + C2  V2)  ( V1 + V2 ).
b) Montrer que la conductivité σ du mélange est σ = ( σ1  V1 + σ2  V2 )  ( V1 + V2 ). Pourquoi σ < σ1 + σ2 ?