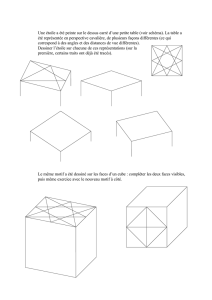
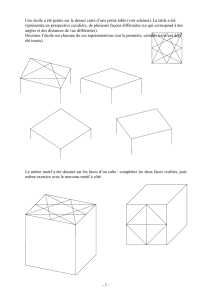
Enoncé de l`exercice

Sections d’un cube – Page 1 - Stage Nouveaux programmes de Seconde – Nicole Vogel – 7 juin 2000
Fiche d’accompagnement de l’activité :
Sections d’un cube avec Geospacw
Cette activité est accompagnée des fichiers de figures Geospacw : « Cube1 »,
« Cube2 », « Cube3 » et « Cube4 ».
Il est possible de les faire réaliser par les élèves ou de les utiliser tels quels.
Dans ce dernier cas, il suffit de cliquer sur l’icône du fichier. Aucune connaissance de Geospacw n’est
nécessaire.
Cependant il est indispensable que le logiciel de géométrie Geospacw soit installé sur votre ordinateur.
 « Cube1 » donne la section d’un cube par un plan (IJK) où I, J, K sont respectivement des points des
plans xOy, yOz, xOz. Il est bien sûr possible de déplacer les points I, J, K avec la souris.
 « Cube2 » donne la section d’un cube par un plan (IJK) où I, J, K sont respectivement des points des
droites (Ox), (Oy) et (Oz). Les points I, J, K peuvent être déplacés.
 « Cube3 » donne la section d’un cube ABCDEFGH par un plan (p) passant par P et parallèle au plan
(AFH). On peut déplacer le point P.
 « Cube4 » est une variante de « Cube3 » dans laquelle les droites contenant les arêtes sont dessinées
et les noms des points d’intersection de (p) avec les arêtes sont affichés.
L’activité suivante concerne la figure « Cube3 » ou éventuellement « Cube4 ».

Sections d’un cube – Page 2 - Stage Nouveaux programmes de Seconde – Nicole Vogel – 7 juin 2000
Sections d’un cube avec Geospacw
Enoncé de l’exercice :
Voici une figure Geospacw. (Figure « Cube3.g3w » ou « Cube4.g3w »)
Elle représente un cube ABCDEFGH.
P est un point de la droite (EH).
Le polygone rose (P0) est l’intersection, lorsqu’elle existe, du plan (p) passant par P et parallèle au
plan (AFH).
Déplacer le point P sur (EH), observer, puis répondre aux questions suivantes :
1) Quelles sont les différentes sortes de polygones (P0) possibles lorsque P parcourt (EH) ?
Quelles sont toutes les positions de P pour lesquelles (P0) est un triangle ?
2) Dans cette question, on choisit P sur [EH] et on note EP = d.
On note Q le sommet de (P0) situé sur [EF] et R son sommet situé sur [AE].
a) Prouver que (PQ) est parallèle à (FH).
b) Dans le plan (EFG), représenter en vraie grandeur EFGH et placer les points P et Q.
c) Prouver que EPQ est un triangle rectangle isocèle. Calculer PQ en fonction de d.
d) Quelle est la nature du triangle PQR ?
3) Dans cette question, on choisit P pour que (P0) soit un hexagone.
a) On note l’hexagone IJKLMN. Prouver que ses côtés sont parallèles à (AF), (AH) ou (FH).
b) Observer la figure Geospacw dans le plan (p) (avec le bouton plan isolé – plan p).
Déplacer le point P et faire une conjecture sur sa position pour que (P0) soit un hexagone régulier.
c) Dans le plan (EFG), représenter en vraie grandeur EFGH. Placer le point P sur (EH) à la
position conjecturée au b).
Prouver qu’alors L et K sont les milieux de [FG] et [GH].
Prouver que (P0) est un hexagone régulier.
A
BC
D
E
F G
HP
A
BC
D
E
F G
HP
L
K
I
J
M
N