La loi de l`offre et la demande - Site de Mohamed Amine EL AFRIT

1
Conservatoire National des Arts et Métiers
Corrigé Exercices Dirigés – La loi de l’offre et la demande
Exercice 1 :
1) L’envoyé de Jules César a-t-il selon vous bien compris la loi de l’offre et de la demande ?
L’employé de Jules César n’a visiblement pas compris la loi de l’offre et de la demande. En
effet, si l’offre ne peut pas satisfaire la demande, le prix ne va pas baisser mais au contraire
augmenter. C’est ce que l’on voit sur le graphique suivant. Si au prix actuel (p1 sur le
graphique) auquel est vendu un menhir l’offre ne peut satisfaire la demande, c’est qu’il y a
un excès de demande. On constate sur le graphique, que si l’offre n’augmente pas,
l’ajustement se fera par le prix qui augmentera jusqu’à p2.
Exercice 2 :
1) C’est le graphique 1. Le départ des touristes a pour effet de déplacer la fonction de
demande vers la gauche, d’où une baisse du prix d’équilibre de 8 à 7 euros.
2) C’est le graphique 4. L’afflux d’offreurs déplace la fonction d’offre vers la droite, ce qui a
pour effet de faire baisser le prix d’équilibre de 7 à 6 euros.
Exercice 3 :
1) La crise a affecté négativement la demande de viande bovine : graphique 1
2) L’abattage massif des troupeaux suspects a un effet sur l’offre du marché : graphique 4
Exercice 4 :
1) Si, simultanément, la demande se déplace vers la gauche et l’offre se déplace aussi vers
la gauche, l’impact sur le prix d’équilibre est indéterminé. Le prix sera plus élevé si la baisse
de l’offre a été plus importante que la baisse de la demande (situation rouge). Inversement,
il sera plus faible si la baisse de l’offre a été moins importante que la baisse de la demande
(situation verte).
Quantité de menhirs
Prix d’un menhir
Offre
Demande
Excès de demande
p1
p2

2
2) On peut imaginer que la demande va se déplacer vers la droite, les consommateurs
d’œufs désertant le marché traditionnel et se tournant vers le marché des œufs biologiques.
L’offre ne devrait, à court terme, pas être affectée. Ceci devrait se traduire par une hausse
du prix des œufs biologiques.
Exercice 5 :
1) La mauvaise récolte implique un déplacement de la fonction d’offre vers la gauche ; le fait
que des consommateurs se tournent vers le marché de la farine de maïs conduit à un
déplacement de la fonction de demande de blé vers la gauche.
2) Il se pourrait que le prix varie assez peu, comme indiqué sur le graphique (cela dépend de
l’ampleur du déplacement des deux fonctions).
Exercice 6 :
Demande
Offre
Demande
Offre
quantité
Quantités en tonne
Prix en euros
Offre 2002
Demande 2002
Prix 2002

3
1) Hypothèse 1 : Dans ce cas, le prix variera peu ou pas du tout
2) Hypothèse 2 : Les producteurs redoutent que le prix de l’aluminium diminue.
Exercice 7 :
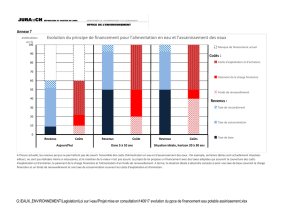
1) Le prix d’équilibre est de 10 euros le pack de 12 bouteilles d’eau minérale. A ce prix,
8000 packs sont vendus et achetés sur le marché.
2) L’introduction de la taxe modifie l’équilibre (nouvelle courbe d’offre en rouge).
Graphiquement, le nouveau prix d’équilibre est d’à peu près 10,5 euros le pack et la
quantité échangée est d’à peu près 7500 packs.
Offre
Demande
Offre
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Quantité
Prix

4
3) Si le prix est de 10,5 euros le pack, la taxe est supportée à égalité par les producteurs et
les consommateurs. Le prix initial était de 10 euros le pack et la taxe est d’1 euro, donc un
prix de 10,5 euros implique que la moitié de la taxe (0,5 euro) est supportée par les
consommateurs (et donc l’autre moitié par les producteurs).
Exercice 8 :
1)  Ce sont les producteurs qui supportent l’intégralité de la taxe (offre totalement
inélastique) ;  Ce sont les consommateurs qui supportent l’intégralité de la taxe (demande
totalement inélastique) ;  Les deux supportent la taxe mais les producteurs en supportent
la majorité (offre plus inélastique que la demande) ;  Les deux supportent la taxe mais les
consommateurs en supportent la majorité (demande plus inélastique que l’offre) ;  La
charge de la taxe est supportée à égalité par les producteurs et les consommateurs (offre et
demande de même pente – en valeur absolue)
2) L’Etat taxe des secteurs dans lesquels la demande est inélastique de façon à ce que la
taxe ne réduise pas les quantités achetées et qu’ainsi la recette fiscale soit maximisée.
3) Si l’Etat utilise la taxe pour réduire la consommation d’un bien polluant, cette mesure sera
d’autant plus efficace que la demande réagira fortement (à la baisse) à une hausse du prix,
donc qu’elle sera très élastique. C’est à la figure 3 que la demande est la plus élastique (la
plus horizontale).
Exercice 9 :
1) Représentez les fonctions d’offre et de demande sur un même graphique.
Pour QO(p) : si p=1/3 Q=0 ; si p=1 Q=2 ; si p=2 Q=5 ; si p=3 Q=8
Pour QD(p) : si p=0 Q=11 ; si Q=0 p=11
0
1
2
3
4
5
6
7
8
9
10
11
12
012345678910 11 12
Quantité
Prix
2) Graphiquement, on voit que le prix d’équilibre est égal à 3 euros du kilomètre et la
quantité d’équilibre est égale à 8 millions de kilomètres.
Exercice 10 (instauration d'un prix plancher) :

5
1)
2) Le prix est donc de 5 euros et la quantité échangée de 25 tonnes.
3) Le surplus des consommateurs (Sc) correspond au triangle supérieur (vert) et le surplus
des producteurs (Sp) au triangle rouge. Sc = [(25 – 5)  20]/2 = 200 ; Sp = [5 20]/2 = 50.
Le surplus total sera donc : St = 200 + 50 = 250.
4)
a) Si p = 8, l’offre sera de 32 tonnes mais la demande ne sera que 17 tonnes. Ce ne
sont donc que 17 tonnes qui seront échangées.
b) S’c = [(25 – 8)  17]/2 = 144,5 ; Sp = [(8 – 4,25)  17] + [4,25  17]/2 = 98,875
; S’t = 144,5 + 98,875 = 244,375.
c) Le surplus des producteurs augmente car la hausse du prix compense la baisse des
quantités vendues. Pour la même raison, le surplus des consommateurs baisse. Le surplus
total diminue car le gain des producteurs (+ 48,875) est inférieur à la perte des
consommateurs (- 55,5). On retrouve un résultat habituel : dès que le prix diffère du prix
d’équilibre, il y a une perte nette de surplus.
Exercice 11 (instauration d'un prix plafond) :
1) Sur ce marché, le prix d’équilibre est de 5 € (200 – 20p = - 50 + 30p  50p = 250  p
= 5). Donc un prix plafond de 6 € n’aura aucun impact puisqu’il n’est pas atteint.
2) En revanche, au prix de 3 €, la demande sera de 140 (200 – 20*3) et l’offre de 40 (- 50 +
30*3). Parmi les 140 de demande, 100 ne pourront ainsi être satisfaits.
Exercice 12 :
1) Qo(p) = Qd(p)  p + 14 400 = 15 740 – p  2p = (15 740 – 14 400)  p = 670
2)a)
b) Chaque entreprise choisit la quantité qui égalise le prix au coût marginal, soit q
= 7. Le profit de chaque entreprise sera : (7*670) – 3 010 = 1 680.
Quantités 1 2 3 4 5 6 7 8 9 10
Cout total 900 1200 1440 1680 1950 2340 3010 4080 5580 7600
CM
Cm
900
600
480
420
390
390
430
510
620
760
390
670
1070
1500
2020
-
300
240
240
270
0
5
10
15
20
25
0 5 10 15 20 25 30 35 40 45 50
Quantités
Prix
Offre
Demande