TP chute libre verticale analyse de la vidéo Ouvrir le fichier chute

TP CHUTE LIBRE VERTICALE
1. analyse de la vidéo
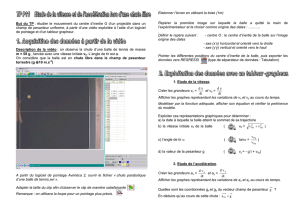
Ouvrir le fichier chute libre sans vitesse initiale présent dans vos documents en consultation.
Enregistrer ce fichier dans votre dossier personnel de travail avant de le modifier.
L'objectif du travail qui suit est d'étudier le mouvement de chute libre d'une balle par
pointage des positions de la balle sur les images successives d'une vidéo.
Un soin très particulier doit être apporté au pointage du centre de la balle avec la souris.
Agrandir au maximum la fenêtre vidéo puis activer l’analyse vidéo .
Pour définir l’échelle, activer le bouton et tracer un trait le long de la règle entre les 2
bandes blanches puis indiquer la longueur de cette règle : 2,00 m.
Sélectionner l’image correspondant au début du mouvement (la dernière image où la balle est
tenue dans la main). Pour définir cet instant comme l’origine du temps, activer la
synchronisation , indiquer 0,00s pour l’heure du graphe.
Activer le pointage puis pointer les positions successives du centre de la balle avant
qu’elle ne touche le sol.
Effectuer une réorganisation automatique de la page.
Afficher le repère dans lequel les coordonnées ont été mesurées . Choisir l’origine de
telle manière que les coordonnées initiales du centre d’inertie de la balle soient (0,0).
Orienter le repère de telle manière que l’axe Oz soit vertical (donc selon la trajectoire de la
balle) et dirigé vers le haut (on tourne le repère à l’aide du rond jaune qui indique l’axe
Ox ).
2. Etude de la position.
Dans le tableau de données, double-cliquer sur y puis renommer la grandeur z. En effet , le
plus souvent l'axe Oz est choisi comme axe vertical.
Afficher le graphe z = f(t) . L’expression théorique de z(t) en fonction du temps, que l’on
peut déduire de la 2ème loi de Newton est : z = - ½ . g . t2 , où g est l’intensité de pesanteur
(g = 9,81 N/kg = 9,81 m.s-2).
Effectuer une « modélisation » (menu « analyse ») par une parabole du type z = a. t2 +b.
Le logiciel trace la parabole la plus proche des points expérimentaux et calcule les
coefficients a et b.
A partir du coefficient a calculé par le logiciel, retrouver une première valeur expérimentale
de g. Calculer l'écart relatif entre cette valeur expérimentale et sa valeur théorique.
Un écart inférieur à 3% sera considéré comme acceptable.

3. Etude de la vitesse.
Dans l’explorateur de données , supprimer les grandeur vx et vy ( ) car il est bon de
savoir les créer.
Créer une nouvelle colonne calculée ( ) pour vx: coordonnée du vecteur vitesse selon
l'axe Ox . Définir cette grandeur par dérivée(‘’ x ‘’, ‘’temps ‘’). Traduction : dérivée de la
coordonnée de position x par rapport au temps.
Pour cela utiliser le bouton fonctions puis calcul puis dérivée et le bouton variable puis x et
temps
Faire de même pour vz.
Insérer un nouveau graphe et choisir d’afficher vz = f(t) .
L’expression théorique de la vitesse selon l’axe Oz est vz(t) = - g.t .
Effectuer une modélisation de cette grandeur et en déduire une nouvelle valeur
expérimentale de l’intensité de pesanteur g. (pour cette modélisation, ne pas tenir compte
du 1er et du dernier point qui ne sont pas alignés avec les autres à cause du calcul de dérivé
qui nécessite un point avant et un point après.)
Calculer l’écart relatif entre la valeur de g issue de cette modélisation et la valeur théorique
g = 9,81 m.s-2.
Un écart inférieur à 3% sera considéré comme acceptable .
4. Changement de repère
Pour discuter sur une même base, ouvrir le fichier chute 2m finie .
Les expressions des coordonnées z(t) et vz(t) dépendent du choix que l'on fait pour
positionner et orienter le repère Oxz.
Modifier la position de l'origine du repère en cliquant au niveau de l'impact de la balle
sur le sol.
Observer les modifications sur les graphes z(t) et vz(t).
Après avoir remis l'origine à la position initiale de la balle, orienter l'axe Oz verticalement
vers le bas avec le point jaune  .
Origine O sur la position initiale de la balle et
axe Oz orienté verticalement vers le haut
Origine O sur la position initiale de la balle et
axe Oz orienté verticalement vers le bas
Origine O sur la position d'impact au sol et
axe Oz orienté verticalement vers le haut
z = - ½ . g . t2
z = + ½ . g . t2
z = - ½ . g . t2 + 2
vz = + g.t
vz = - g.t
vz = - g.t + 2

5. Etude de l’accélération
Au vu de l’allure de vy = f(t), que peut-on dire de ay ?
Le vérifier en créant cette grandeur.
Comment peut-on qualifier le mouvement de la balle ?
6. Etude d’une chute libre avec vitesse initiale
Brancher la webcam sur une des prises USB de l’ordinateur. Ouvrir un nouveau fichier Logger Pro.
Choisir d’ « insérer » une « capture vidéo ». Aller dans « options » que vous paramétrez comme suit. (5 secondes
suffiront)
Puis dans paramètres appareil, régler le gain au maximum pour avoir le maximum de sensibilité (image trop lumineuse)
puis ajuster la vitesse de l’obturateur Pour avoir une image correcte. Ces réglages permettent que les objets
n’apparaissent pas flous même s’ils sont en mouvement. Choisir 15 images par seconde.
Se placer à au moins 2m de la webcam. Effectuer la mise au point en tournant le bague de l’objectif. Tenir d’une main
une règle d’1m et de l’autre main une balle de golf.

Démarrer la capture vidéo, lancer la balle de golf verticalement vers le haut. Ne pas hésiter à supprimer la vidéo si celle
ci n’est pas satisfaisante, il est facile de recommencer.
Effectuer la même analyse que précédemment après avoir choisi l’origine du repère à la position où la balle est lâchée.
Commencer le pointage un peu avant le lâcher de la balle afin de pouvoir disposer d’une valeur correcte pour la valeur
initiale de vy0 à la date t=0 s correspondant au lâcher de la balle.
Afficher le graphe vy = f(t). Modéliser vy(t). Que vaut vy(t=0s) ? A quel date vy(t) = 0s ? Que vaut y à cette date ?
L’équation horaire théorique d’un tel mouvement est y = -1/2 g.t2 + vy0.t + z0.
Prévoir par la théorie la hauteur maximale atteinte par la balle. Comparer à la valeur expérimentale.