Exercice I : Mécanique Eulérienne pour débutants (4 points)

Exercice I : Mécanique Eulérienne pour débutants (4 points)
Une balle de masse m, de centre d'inertie G, est lâchée sans vitesse, d'une hauteur H = 15,0 m au-dessus d'un sol sablonneux
terrestre. On assimilera la balle à son centre d'inertie G.
O x
z
Le repère d'étude (O, x, z ) est schématisé ci-dessus. On prendra g = 9,81 m.s et la durée de la chute est d'environ 2 s. On
néglige les forces de frottements, lors de la modélisation mathématique (parties 1. et 2. de l'exercice) mais elles peuvent tout de
même exister et avoir une influence sur le mouvement de la balle (partie 3 et 4. de l'exercice). Par contre on néglige la poussée
d'Archimède pour la totalité des questions de l'exercice.
1. Principe d'inertie.
On suppose que la seule force extérieure qui s'exerce sur la balle est le poids
P
1.1. Dans quel référentiel galiléen faut-il traiter le mouvement de cette balle ?
1.2. Citez le principe d'inertie (ou première loi de Newton).
1.3. En déduire que le mouvement de la balle ne peut pas être rectiligne uniforme.
2. Méthode d'Euler
On suppose toujours que la seule force extérieure qui s'exerce sur la balle est le poids
P
. L'application de la seconde loi de
Newton donne la relation suivante :
g
dt
(v d zG )
(1)
où
zG
v
désigne la composante de la vitesse du centre d'inertie de la balle suivant l'axe z (avec le choix de l'énoncé quant à
l'orientation de l'axe (O, z ). On se propose dans ce qui suit d'appliquer la méthode d'Euler au mouvement décrit par l'équation
(1). En effet si t est petit par rapport à la durée de chute on peut écrire
g
Δt
)(v ΔGz 
2.1. Déduire de cette nouvelle écriture, la relation permettant d'exprimer la vitesse
zG
v
(t + t) en
fonction de
zG
v
(t), t et g.
sable
H = 15,0 m
G

On fixe t = 50,0 ms.
2.2. Calculer la valeur de
zG
v
(8 t), sachant que
zG
v
(7 t) = 3,43 m.s .
3. Tracé de vecteurs et vitesse et principe d'inertie
Sur l'annexe (A RENDRE AGRAFEE AVEC LA COPIE) figure un extrait de la chronophotographie (document 1)
du mouvement de la balle entre les instants de date t1 = 1,950 s et t2 = 1,965 s pour lesquels la position du centre d'inertie de la
balle est notée, respectivement, G39 et G42. L'échelle utilisée sur ce document est de 1,0 cm pour 1,0 cm et l'intervalle de temps
entre chaque cliché (photo) vaut = 5,0 ms
3.1. A l'aide de cet enregistrement et uniquement à l'aide de celui-ci, calculer la norme du vecteur vitesse
du centre d'inertie pour la position G40.
3.2. Sur cet extrait d'enregistrement, tracer le vecteur vitesse du centre d'inertie pour la position G40 , avec
l'échelle 1,0 m.s pour 1,0 cm.
3.3. Qualifiez en le justifiant, le mouvement du centre d'inertie de la balle entre les positions G39 et G42.
3.4. En déduire, à l'aide du principe d'inertie, qu'entre ces positions la somme vectorielle des forces
extérieures, au système balle, est nulle. On justifiera la réponse.
On déduit de cette dernière réponse et par comparaison avec la réponse à la question 1.3. qu'au moins une force supplémentaire
est apparue au cours du mouvement. La partie 4. de cet exercice essaie de qualifier cette force.
4. Comparaison avec l'évolution temporelle de la vitesse de la balle au cours du mouvement.
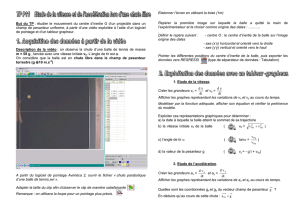
On reporte sur la figure 1 ci-dessous l'évolution temporelle de la vitesse réelle du centre d'inertie (déduite de l'étude
complète de la chronophotographie et dont les valeurs successives sont représentées par des triangles) et l'évolution prédite par la
méthode d'Euler (dont les valeurs successives sont représentées par des carrés)
0,00
5,00
10,00
15,00
20,00
25,00
0 0,5 1 1,5 2 2,5
Figure 1
Afin d'étudier les différences entres ces deux courbes on l'analyse en trois parties (repérées pare des pointillés verticaux sur la
figure 1 ci-dessus) :
Partie de 0 à 0,2 s
Partie de 0,4 à 2,1 s
Partie au-delà de 2,2 s.
4.1. Etude de la première partie.
t (s)
vGz (m.s)
vGz = f(t)

4.1.1. La comparaison des résultats donnés par la méthode d'Euler sur cette première partie et les valeurs
réelles valide-t-elle le choix de t ? On justifiera la réponse.
4.2. Etude de la seconde partie.
4.2.1. Que pensez-vous des résultats donnés par la méthode d'Euler dans cette seconde partie ?
4.2.2. Que peut-on en déduire sur le(s) hypothèse(s) retenue(s) pour établir la relation (1) lorsque la
vitesse du centre d'inertie devient plus élevée que 2,0 m.s ?
4.2.3. Quelle force doit-on prendre en compte afin de mieux rendre compte du phénomène réel ? On
donnera le nom de cette force et son effet sur le mouvement.
4.3. Etude de la dernière partie.
4.3.1. Pourquoi la vitesse est-elle subitement devenue nulle entre les instants de dates t = 2,15 s et t =
2,20 s ?
Si les forces de frottements n'existent pas la relation de Galilée H =
2
1
g.t ² s'applique (où H désigne la distance parcourue
suivant l'axe vertical et "t " la durée de parcours depuis l'instant de date t = 0).
4.3.2. Calculez la durée de la chute, notée tssfrot, si l'on suppose que la formule de Galilée s'applique.
4.3.3. Comparez à la durée réelle de chute, notée tréelle, en déduire que la force ajoutée en 4.2.3. freine (ou
retarde) le mouvement