vitesse et mouvements

VITESSE ET MOUVEMENTS
I – RAPPELS : REFERENTIELS ET TRAJECTOIRES
1- Référentiels
Système : il est constitué du solide dont on étudiera le mouvement. Si les dimensions du solide
peuvent être considérées comme négligeables par rapport aux distances qu’il parcourt ; le solide est
alors assimilé à un point matériel.
Activité : rétrogradation de mars
Référentiel : C’est un solide par rapport auquel , on choisit de décrire le mouvement d’un corps.
Décrire un mouvement n’a de sens que si l’on précise par rapport à quel référentiel ce mouvement est
considéré.
Quelques référentiels :
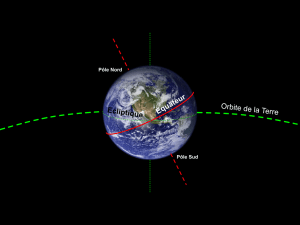
le référentiel terrestre, constitué par la Terre, permet l’étude des mouvements se déroulant à la
surface et au voisinage de la Terre.
Le référentiel géocentrique, constitué par le centre de la Terre et 3 étoiles fixes, permet l’étude
des mouvements de la lunes ou de satellites.
Le référentiel héliocentrique, constitué par le centre du Soleil et 3 étoiles fixes, permet l’étude des
mouvements des planètes.
2- Trajectoire
C’est l’ensemble des positions successives occupées par le point au cours du temps.
Remarque : La trajectoire dépend du référentiel choisi.
On peut repérer la position d’un point M sur la trajectoire, à chaque instant, grâce à des
coordonnées cartésienne x, y et z.
MO 
= x
i
+ y
j
+ z
k
II – VITESSE
1- Vitesse moyenne
La vitesse moyenne est la distance d parcourue par un mobile pendant une durée t :
t
d
Vm 
Vm en m.s-1 ; d en m ; t en s
O
x
y
z
M
i
j
k

2- Vitesse instantanée
La vitesse instantanée est la vitesse à un instant précis. (exemple : vitesse indiquée par un compteur
de voiture)
Calcul approché de vitesse instantanée :
La vitesse instantanée V2 au point M2 est égale à la vitesse moyenne de ce point entre les instant t1
et t3. (t1 et t3 sont très proche de t2).
V2 = M1M3 = M1M3
t3 – t1 2
Remarque 1 : Dans certains cas, on peut confondre la longueur de l’arc M1M3 avec celle du segment
[M1M3].
Vitesse et mouvement :
- Si la vitesse reste constante au cours du mouvement, le mouvement est uniforme.
- Si la vitesse augmente au cours du mouvement, le mouvement est accéléré.
- Si la vitesse diminue au cours du mouvement, le mouvement est décéléré ou retardé.
3- Vecteur vitesse
Le vecteur vitesse
)(tv
permet de définir le mouvement d’un point à l’instant t.
Caractéristiques du vecteur vitesse :
- point d’application : le point M considéré à la date t ;
- direction : tangent à la trajectoire à la date t ;
- sens : celui du mouvement à la date t ;
- norme : valeur de la vitesse instantanée à la date t.
Représentation du vecteur vitesse au point M2 :
Origine : M2
Direction : M1M3
sens : M2 vers M3.
norme : v2 =
21MM
/2 = 0,16 m.s-1
Echelle pour
v
: 1 cm pour 0,1 m.s-1
M1
M2
M3
M4
M5
Les points de la trajectoire ont été définis tous
les  = 60 ms
M0
M1
M2
M3
M4
Les relevés des points M se font tous les  = 60 ms

III – ETUDE DE QUELQUES MOUVEMENTS D’UN SOLIDE
1 – Centre d’inertie
Ce point est le centre géométrique du solide si le solide est homogène. Son mouvement est plus
simple que les autres.
Quelques formes géométriques simples :
- pour une sphère homogène : G est le centre de la sphère
- pour un parallélépipède : G est le centre du parallélépipède
- pour un anneau : G est le centre de l’anneau (n’appartient pas à la matière ; se trouve hors de
l’anneau)
2- Solide en translation
a) Définition
Au cours d’un mouvement de translation, tous les points du solide ont, à chaque instant t, le même
vecteur vitesse
)(tv
.
Attention : ce vecteur vitesse peut varier au cours du temps.
Voir TP
b) Exemples
Translation rectiligne uniforme: (position des mobiles tous les 20 ms)
Le vecteur vitesse est constant au cours du temps.(
)()( 21 tvtv AA
)
A t1, les points A et B ont même vecteur vitesse. (
)()( 11 tvtv BA
)
Translation rectiligne accéléré :
Au cours du temps, le vecteur vitesse est constant en direction et sens mais pas en norme
(
)()( 21 tvtv AA
). Par contre à t1 de même qu’à t2, les points A et B ont même vecteur vitesse
)()( 11 tvtv BA
et
)()( 22 tvtv BA
( solide en translation).
Translation curviligne :
A
B
)( 1 tvA
)( 1 tvB
A
B
)( 2 tvB
)( 2 tvA
A
B
)( 2 tvB
)( 2 tvA
A
B
)( 1 tvA
)( 1 tvB
A
B
)( 1 tvA
)( 1 tvB
B
A
)( 2 tvA
)( 2 tvB
Au cours du temps, le vecteur vitesse varie en direction et
norme.
)()( 21 tvtv AA
mais
)()( 11 tvtv BA
(solide en translation).

2- Solide en rotation autour d’un axe fixe (cf TP)
a) Définition
Un solide indéformable est en mouvement de rotation autour d’un axe fixe si les trajectoires de tous
les points de ce solide sont des arcs de cercle centrés sur l’axe de rotation et contenus dans un plan
perpendiculaire à l’axe de rotation
Seuls les points de l’axe de rotation sont fixes dans le référentiel choisi.
b) Vitesse angulaire 
Pour une vitesse angulaire instantannée au point 1,
220
Exercice :
1) Le compte-tours d’une voiture indique 3000 trs/min. Calculer la vitesse angulaire correspondante
en rad.s-1.
 = (3000 x 2)/60 = 3,14.102 rad.s-1.
2) Un solide est en rotation. Pendant un temps = 20ms, il tourne d’un angle de 10°. Calculer la
vitesse angulaire correspondante en rad.s-1.
 = (10 x /180)/20.10-3 = 8,7 rad.s-1.
c) Relation entre vitesse v et vitesse angulaire 
Soit l l’arc de cercle parcouru pendant l’intervalle de temps .
l = R (R rayon du cercle)
Or v = l/ = R/ = R
R
v
Remarque :
Tous les points d’un solide en rotation ont :
- la même vitesse angulaire 
- une vitesse instantanée v telle que v = R. (R étant la distance du point considéré à l’axe de
rotation)
Exemple : pour M1 on a v1 = R1.
pour M2 on a v2= R2. et comme R2 > R1 on a v2 > v1
d) Rotation uniforme
Un solide est animé d’un mouvement de rotation uniforme si  = cste.
Pour un point du solide, le vecteur vitesse
v
varie en direction et sens ; il est constant en norme.
La durée pour effectuer un tour est constante : le mouvement est dit périodique.
 en radian angle dont a tourné le solide pendant l’intervalle
de temps .
 en s
 en rad.s-1
ou v = R
R1
R1
R2
l
M2
M1
A 2
A 1
A 0
0-2

La période T du mouvement de rotation uniforme est égale à la durée d’un tour.
Si un tour  = 2. rad
 = 1.T  =  / = 2. /T
2 T
L’inverse de la période est la fréquence f du mouvement :
T
1
f