1 TSMP Cours Physique Chap 4 : Les bobines, l`auto

1
TSMP Cours Physique
Chap 4 : Les bobines, l’auto-induction et le dipôle (R,L)
Dans le chapitre précédent, nous avons vu que toute variation de flux magnétique à proximité d’un
conducteur faisait apparaitre une fém d’induction aux bornes du conducteur ou un courant induit si le
circuit est fermé. On distinguait alors clairement un inducteur extérieur provoquant la « cause »
(aimant, bobine…) et un induit subissant les « effets » (conducteur ou circuit).
Mais, une bobine parcourue par un courant crée son propre champ magnétique. Si celui-ci varie, elle
va provoquer des phénomènes d’induction appelées ici auto-induction car l’inducteur et l’induit
sont confondus. C’est ce que nous allons étudier ici.
I. Quelques notions d’électricité Révisions (2min21) : http://www.wideo.fr/video/iLyROoafttp1.html
D’autres rappels : tension (2min18) : https://www.youtube.com/watch?v=Hvpt6p0ikuA
L’intensité (1min52) : https://www.youtube.com/watch?v=KYYw9PYOTKg
1) Conventions d’écriture
En électrocinétique (électricité), les lettres minuscules désignent des grandeurs ……………………………….. (i, q, t, u…)
et les lettres MAJUSCULES des grandeurs …………………………. (ou continues : I, Q, T, U…).
Ex : on écrit : ………………………………………….
2) Loi d’Ohm généralisée
Considérons une portion de circuit électrique quelconque (AB).
On choisit un sens positif (+) : de A vers B.
D’après ce choix : iA→B = iAB > 0 et iB→A = iBA < 0.
La tension entre les points A et B est notée uAB = VA – VB
Attention : la flèche qui la représente est orientée de … vers …
Dans le cas le plus général, il existe une relation entre :
- la tension uAB aux bornes de la portion de circuit,
- l’intensité du courant iAB parcourant cette portion de
circuit,
- la résistance électrique totale de la portion de circuit RAB,
- la fém totale eAB existant (ou non) entre les points A et B.
Cette relation est appelée : « loi d’Ohm généralisée ».
Loi d’Ohm généralisée :
Rem 1 : le signe de iAB dépend du sens (+) choisi. En pratique, si on connait le vrai sens du courant (le sens conventionnel), on
choisit le sens (+) dans le même sens pour avoir iAB > 0.
Rem 2 : RAB > 0 toujours puisque cela représente la valeur d’une résistance !
Rem 3 : eAB peut être > 0 ou < 0 suivant que cette fém tend à faire circuler un courant dans le sens (+) ou en sens contraire.
Rem 4 : uAB peut être > 0 ou < 0 suivant les valeurs et les signes de RAB, iAB et eAB.
a) Cas d’un conducteur ohmique (résistor)
La portion de circuit (AB) ne comporte qu’un résistor de
résistance R et des fils dont la résistance est considérée nulle.
Dans ce cas simple : RAB = ……….. , eAB = …………..
et la loi d’Ohm généralisée s’écrit : …………………………..
u
t
Um
T
Dipôle quelconque
A
B
iAB
(+)
uAB
résistor (R)
A
B
iAB
(+)
uAB

2
b) Cas d’un dipôle générateur
La portion de circuit (AB) comporte un générateur (ex : pile)
de résistance interne r et de fém notée E > 0.
La fém fournit un courant électrique d’intensité i dont le sens
conventionnel est du pôle + au pôle – à l’extérieur du
générateur.
Choisissons le sens (+) dans le même sens pour avoir iAB > 0.
Dans ce cas : RAB = ……….. , iAB = ………….. , eAB = ………….. et la loi d’Ohm généralisée s’écrit : …………………………..
En notant P le pôle Positif du générateur et N le pôle Négatif, on a alors UPN = ………………………………………………
Ainsi la fém correspond à la tension positive aux bornes du générateur lorsque i = 0 ou tension « à vide ».
C’est la valeur maximale de la tension qu’il pourrait donner (s’il n’avait pas de résistance interne).
c) Cas d’un dipôle récepteur
La portion de circuit (AB) comporte un récepteur (ex : moteur,
électrolyseur (piles « rechargeable »), lampe…) de résistance
interne r’ et de force contre-électromotrice fcém notée E’ > 0.
Le récepteur transforme une partie du travail électrique qu’il
reçoit en une énergie d’une autre forme : énergie mécanique pour
le moteur, énergie chimique pour l’électrolyseur, travail
rayonnant pour la lampe… Le reste est perdu en chaleur dans le
récepteur à cause de sa résistance interne (effet Joule).
Choisissons le sens (+) dans le même sens que le sens conventionnel i du courant.
Dans ce cas : iAB = …… reçue par le récepteur est > 0 , RAB = ………..
On admet que eAB < 0 : en effet le récepteur tend à faire circuler un courant dans le sens contraire de i. Ceci peut se comprendre par
le phénomène d’induction pour les moteurs (loi de Lenz) ou en imaginant une « pile rechargeable donc branchée à l’envers »…
On pose eAB = - E’ et la loi d’Ohm généralisée s’écrit : ……………………………………………………………………….
Ainsi la fcém correspond à la partie de la tension aux bornes du récepteur qui est réellement utile (et convertie en autre chose
qu’en chaleur à cause de la résistance interne du récepteur).
II. L’auto-induction
1) Mise en évidence expérimentale
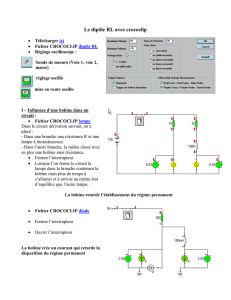
a) Fém d’auto-induction
 Observation : on ferme l’interrupteur K. La lampe L1
brille ………………………………… mais la lampe L2
s’allume ………………………………. : le courant i1
s’établit donc ………………………………… mais i2
ne s’établit que …………………………………. .
Conclusion : la bobine tend donc à …………………………………. à l’établissement du courant dans sa branche.
Expérience en vidéo (1min22) : https://www.youtube.com/watch?v=isllsO6aqrc
(E > 0 , r)
A
B
iAB
(+)
uAB
N
P
+
−
(E’ > 0 , r’)
récepteur
A
B
iAB
(+)
uAB
i
Interrupteur K
Lampe L1
Lampe L2
Résistor R
Bobine
i1
i2

3
 Interprétation : i2 variant de 0 à sa valeur maximale crée dans la bobine un flux magnétique propre variable, ce qui produit
une fém d’induction appelée ici fém ………………………….…………… car c’est la variation du courant dans le circuit
lui-même qui lui donne naissance.
 Généralisation :
Une fém ……………………………….……… prend naissance dans un circuit (ou bobine) parcouru(e) par un courant d’intensité
variable. Elle est due à la variation du flux magnétique …………………….. du circuit (bobine).
Rem : l’inducteur et l’induit sont ici ……………………………… : c’est le circuit lui-même d’où le nom d’auto-induction.
b) Courant d’auto-induction
Le circuit étant fermé, la fém d’auto-induction fait apparaître un courant induit qui, d’après la loi de Lenz, tend à …………………
à l’établissement du courant i2 qui lui donne naissance.
Il est donc en sens …………………….. et, au début, l’intensité totale traversant la lampe L2 est insuffisante pour la faire briller.
Ensuite, la variation du courant i2 devient plus lente et le courant induit s’annule progressivement : la lampe L2 peut donc briller.
Le courant induit, appelé ici courant …………..…………….……………………… tend à ………………….…………… à la
………………………… du courant qui lui donne naissance.
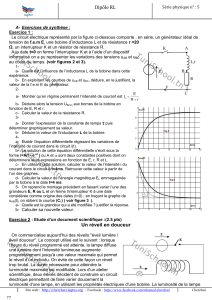
c) Comportement d’une bobine
On considère le circuit suivant :
Le Générateur Basses Fréquences (GBF) fournit une tension « en
créneau » entre 0 et E = 2,0 V à une certaine fréquence f = 200 Hz.
La résistance R du conducteur ohmique vaut R = 1000 .
Définition :
Le point M correspond à la masse du circuit (symbole : )
c’est-à-dire à un point dont le potentiel électrique vaut 0 V par
définition VM = 0 V.
 Quelle est la tension visualisée sur la voie A de l’oscilloscope ?
 Représenter son allure sur l’oscillogramme à droite.
 Quelle est la tension visualisée sur la voie B de l’oscilloscope ?
Quel est l’intérêt d’observez cette tension ?
 Représenter son allure sur l’oscillogramme à droite.
i
Y
A
Y
B
M
B
A
GBF
Bobine
R
u
G
Conclusion :
le courant ne s’installe
pas et ne s’annule pas
……………………… :
(t’0 ≠ t0 et t’1 ≠ t1).

4
Une bobine tend à s’opposer aux variations (établissement et annulation) du …………………………… du circuit dans lequel
elle se trouve. L’intensité du courant qui traverse une bobine n’est donc jamais ……………………………
2) Valeur de la fém d’auto-induction : loi de Faraday-Lenz
a) Dispositif expérimental
On considère le circuit suivant :
Le GBF fournit une tension « triangulaire » entre – 2 V et + 2,0 V
à une certaine fréquence f = 200 Hz.
La résistance R du conducteur ohmique vaut R = 10 k.
La résistance interne de la bobine r est quasi nulle : r 0.
Pour une même sensibilité verticale, on constate que :
uBM (voie B) ………. uAM
Or, d’après la loi d’additivité des tensions : uAM = ……………..
donc uAB = ……………… ………..
Mais, d’après la loi d’Ohm généralisée : uAB = ………………
 Sur la voie A, on observe donc la ………………………………………………. mais aussi l’allure de
…………………………… (au facteur R près).
 Sur la voie B, on observe donc la …………………………………………………………
Mais, d’après la loi d’Ohm généralisée : uBM = ……………………
Dans ce cas : RBM = ……………........ , iBM = …….. , eBM = ………..…. : fém d’auto-induction, seule fém existant entre les points B
et M. Donc la loi d’Ohm généralisée s’écrit : uBM = …………………………..
Finalement, sur la voie B on observe ……………………………………………………………………
b) Etablissement expérimental de la loi de Faraday-Lenz
voie A : uAM R*i
Entre 0 et T/2 on observe, sur la voie A, une portion de ………………..…… croissante dont
la dérivée est une ……………………………………… et sur la voie B une valeur
…………………………………………….
Entre T/2 et T on observe, sur la voie A, une portion de ………………….. décroissante dont
la dérivée est une ……………………………………… et sur la voie B une valeur
…………………………………………….
voie B : uBM = - e
De même pour toutes les périodes qui se succèdent.
Conclusion : le signal de la voie B est donc proportionnel à la …………………… du signal
de la voie A.
On peut alors écrire : ……………………………………………………………………….
Donc la fém e = …………………………….
i
Y
A
Y
B
M
B
A
GBF
Bobine
r 0
R = 10 k
u
G
(+)

5
Le coefficient de proportionnalité k’, caractéristique de la bobine, est appelé ………………………………………………………..
ou encore ………………………….. de la bobine. On le note L. Sa valeur est en …………………….. de symbole …………..
Rem : l’inductance L ne dépend que des caractéristiques de la bobine (longueur, diamètre, nombre de spires…) ; c’est donc une
constante pour une bobine donnée.
Loi de Faraday-Lenz :
La fém d’auto-induction e est proportionnelle à ………………………………….. L de la portion de circuit (bobine) et à la
……………………..….. par rapport au temps de ………………………………. du courant qui parcourt le circuit (bobine) :
Préciser les unités des grandeurs intervenant dans cette relation.
Rem : le signe « - » présent dans la formule traduit la loi de Lenz :
 Si i ,
dt
di
L.
……….. et e ………… crée un courant induit dans le sens ……………….….. de i (+)
Ce courant induit se retranche au courant initial et donc i ……
 Si i ,
dt
di
L.
……….. et e ………… crée un courant induit dans le ………………. sens que i (+)
Ce courant induit s’ajoute courant initial et donc i ……
c) Flux propre et inductance
Nous voulons trouver l’expression du flux magnétique propre d’une bobine (ou une portion de circuit) d’inductance L. Pour cela,
écrivons la loi de Faraday-Lenz sous 2 formes différentes :
e = …………………………………………………………………………… car L est une constante pour une bobine donnée.
Par identification, on trouve : ……………………………………..
Le flux propre d’une portion de circuit (bobine) appelé flux ………………………………………. est proportionnel à
……………………………………… L de la portion de circuit (bobine) et à ………………………………. du courant qui
parcourt le circuit (bobine) :
Rem 1 : Φ = N*
B
*
S
= N*B*S*cos  i B  i : l’intensité du champ magnétique créé par un circuit parcouru par un
courant (bobine) est proportionnelle à l’intensité du courant. On retrouve un résultat exposé en 1ère S, qui n’est valable qu’en
l’absence de matériau ferromagnétique (noyau de fer doux).
Rem 2 : physiquement, l’inductance L d’une portion de circuit (bobine) correspond au coefficient de proportionnalité entre son
flux propre et l’intensité du courant qui la traverse. Il mesure en quelque sorte, l’« efficacité d’une bobine à créer un flux
magnétique (donc un champ magnétique) pour une intensité donnée ».
Rem 3 : d’après nos conventions, Φ et i sont toujours de même signe : les inductances L sont donc toujours > 0.
Exo 1 : représenter un courant i dans le sens (+) choisi.
Représenter les vecteurs
B
et
S
.
Quel est le signe de i : …….
Quel est le signe de Φ : ……. En déduire le signe de L : ……
Exo 2 : représenter un courant i dans le sens inverse du sens (+)
choisi. Représenter les vecteurs
B
et
S
.
Quel est le signe de i : …….
Quel est le signe de Φ : ……. En déduire le signe de L : ……
(+)
(+)