exo_fiabilite02m

Les probabilités seront données sous la forme décimale arrondie à
3
10-
près.
La fonction de fiabilité d’un composant C est définie par : R (t) =
0,0125
et
, (t en jours).
On note X la durée de vie aléatoire (en jours) du composant C.
1) Quel est le temps moyen de bon fonctionnement du composant C ?
2) Quelle est la probabilité que le composant C fonctionne encore au bout de 60
jours ?
3) Au bout de combien de jours la fiabilité deviendra t-elle inférieure à 0,1 ?
4) Un dispositif utilise 4 composants C identiques, fonctionnant simultanément et
de manière indépendante. Le dispositif est opérationnel si au moins 3 de ces
composants fonctionnent.
On note F le nombre aléatoire de composants qui fonctionneront encore dans
60 jours, et on admet que F suit la loi binomiale B (4 ; 0,47).
Quelle est la probabilité que le dispositif soit opérationnel dans 60 jours ?
Correction
Exercice II
1)
La MTBF est
1
, avec ici
0,0125=
. La MTBF est donc égale à 80 jours.
2
2)
La probabilité demandée est donnée par :
( ) ( )
0,0125 60 0,75 3
P X 60 60 e e 0,472 (valeur arrondie à 10 près).R- ´ - - > = = = =
2
3)
( )
0,0125 ln10
0,1 e 0,1 0,0125 ln0,1 .
0,0125
ln10 184,2 : la fiabilité deviendra inférieure à 0,1 à partir de 185 jours.
0,0125
t
R t t t
-
< Û < Û - < Û >
»
3
4)
Le dispositif est encore opérationnel au bout de 60 jours si F
3³
.
( ) ( ) ( ) ( ) ( ) ( ) ( )
3 1 4 0
34
44
P F 3 P F = 3 P F = 4 0,47 0,53 0,47 0,53 0,269.CC³ = + = ´ + ´ =
3
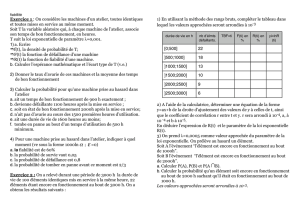
EXERCICE N° 2
(10 points)