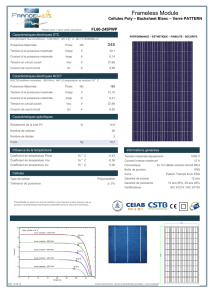
AMPLIFICATEUR_DIFFERENTIEL_CMOS_2

Débiton Nicolas
Marques William
1 - 9
AMPLIFICATEUR DIFFERENTIEL CMOS 2 :
MESURES
But du TP : retrouver les caractéristiques pour divers fonctionnements (différentiel et mode
commun) d’un CMOS de manière pratique afin de les comparer aux résultats théoriques
déterminés au TP précédent (CMOS simulation).
1. Etage différentiel polarisé par résistance
1.1 Point de repos
Nous désirons retrouver les valeurs de VGS20, VGS30, VDS20, VDS30 ainsi que ID20 et ID30 et les
comparer aux valeurs obtenues en simulation. Nous réalisons le schéma ci-dessus en fixant
Ve1=Ve2=0 pour déterminer le point de repos.
Transistor MN2
Transistor MN3
VGS20 = - 3,5 V
VGS30= - 3,5 V
VDS20= - 0,6 V
VDS30= - 0,6 V
ID20= 0,23 mA
ID30= 0,23 mA
Le courant ID20 se trouve de la manière suivante : il faut relever la valeur de la tension aux
bornes de RD1 et la diviser par la valeur de la résistance.
mA
R
U
I
D
RD
D23,0
10^10 3,2 3
1
1
20 
.
De plus nous sommes en présence de même transistor dont le drain est connecté à des
résistances équivalentes, c’est pourquoi les valeurs des VGS, VDS et ID sont quasiment égales.
1.2 Fonctionnement en mode différentiel
Rappel : Tension de mode commun
21 eemd VVV 

Débiton Nicolas
Marques William
2 - 9
Tension de mode différentiel
221 ee
mc VV
V
En mode différentiel pur, nous avons Ve1=-Ve2, d’où Vmc=0V.
a. Nous voulons exprimer Vmd et Vmc en fonction de Ve1.
e2 est relié à la masse (Ve2=0V) tandis que Ve1 est une tension sinusoïdale de fréquence
100 Hz et d’amplitude 0.4V.
Dans ce cas les expressions ci-dessus deviennent alors :
1emd VV 
et
21e
mc V
V
.
b. Nous mesurons l’amplification de mode différentiel Ad.
5,5
9,0 5
21
21 
ee
SS
dVV VV
A
En simulation, nous avions trouvés une amplification
2,4
d
A
.
c. Nous allons maintenant calculer la valeur théorique de l’amplification afin de la
comparer à la valeur obtenue en simulation et en pratique.
Pour calculer la valeur de Ad en fonction de RD et de gm nous allons nous intéresser au
montage en petit signaux du circuit. Après simplification nous obtenons le circuit suivant.
Nous pouvons alors en déduire les équations suivantes :
Intéressons nous tout d’abord aux équations qui régissent les entrées :
SGSmGSmGSeRVgVgVV ).(2111 
SGSmGSmGSeRVgVgVV ).(2122 
D’où
2121 GSGSee VVVV 
Déterminons ensuite les équations de sortie :
)())(( 212121 GSGSmGSmGSmdSSs VVgVgVgRVVV 
Nous pouvons alors déterminer l’équation de l’amplification différentielle qui
est définit par :

Débiton Nicolas
Marques William
3 - 9
21
21
ée
SS
dVV VV
A
D’où
5)(. 21  eedmd VVRgA
Nous retrouvons bien le résultat trouvé avec les simulations :
5
d
A
.
1.3 Fonctionnement en mode commun
Pour augmenter et mesurer plus facilement l’amplification de mode commun
C
A
, nous
introduisons une dissymétrie dans l’étage différentiel en rajoutant une résistance de
470Ω en série avec
1D
R
et nous appliquons sur les entrées une tension sinusoïdale de
fréquence 100Hz et de faible amplitude.
Dans cette partie, nous relions les entrées e1 et e2 de l’amplificateur différentiel.
Nous allons mesurer l’amplification en mode commun.
05,0
2
21
21
2121 
e
SS
ee
SS
mc
SS
mc VVV
VV VV
VVV
A
Connaissant la valeur de l’amplification différentielle et l’amplification en mode
commun, nous pouvons déterminer la valeur du taux de réjection en mode commun.
100
05,05
mc
d
A
A
TRMC
Soit en décibels :
dBTRMCdBTRMC 40)log(20)( 
2. Etage différentiel polarisé par une source de
courant
Nous remplaçons la résistance RS de la première partie par une source de courant réalisée à
l’aide d’un transistor NMOS MN1 identique aux transistors de la paire différentielle.
2.1 Point de repos
Dans cette partie, nous considérons que les entrées sont reliées à la masse
0
21  ee VV
et
R1=150kΩ.
Nous désirons obtenir les mêmes courants de repos qu’avec la polarisation par résistance.
Dans la partie précédente, nous avons trouver la valeur du courant
mAIDO 23,0
.

Débiton Nicolas
Marques William
4 - 9
En utilisant la caractéristique
)( GSDVfI 
, tracée en simulation, nous déterminons la valeur
de la tension VGS pour le transistor MN1.
Nous trouvons VGS=2,75V.
De plus, la tension Vdd=5-(-5)=10V.
En utilisant la méthode du pont diviseur, nous pouvons déterminer la valeur de R2.
21
2
1.RR VR
Vdd
GS 
d’où
k
VV RV
R
GSdd
GS 56
75,210 3^10.150.75,2. 1
2
Nous allons relevés les tensions VGS20, VGS30, VDS20, VDS30 et les courants ID20, ID30 afin de
vérifier si nous obtenons les mêmes points de repos qu’avec le montage précédent.
Transistor MN2
Transistor MN3
VGS20 = 3,6 V
VGS30= 3.6 V
VDS20= 5 V
VDS30= 5 V
ID20= 0,21 mA
ID30= 0,22 mA
VGS
0V 0.5V 1.0V 1.5V 2.0V 2.5V 3.0V 3.5V 4.0V 4.5V 5.0V
ID(M1)
0A
0.5mA
1.0mA
1.5mA
2.0mA
ID=0,23mA
VGS=2,75V

Débiton Nicolas
Marques William
5 - 9
Les valeurs des courants sont identiques à celles trouvées avec le montage par polarisation
avec résistance, le point de polarisation reste donc inchangé.
2.2 Fonctionnement en mode différentiel
Nous désirons effectuer la même étude que précédemment (1.2) afin de la comparer à la
valeur théorique.
En mode différentiel pur, nous avons Ve1=-Ve2, d’où Vmc=0V.
Ve2=0V tandis que Ve1 est une tension sinusoïdale de fréquence 100 Hz et d’amplitude 0.4V.
De la même manière (rapport entre sorties et entrées) nous en déduisons l’amplification en
mode différentiel.
75,4
4,09,1
21
21 
ee
SS
dVV VV
A
En théorie, l’amplification valait -4.3, aux incertitudes de mesures près, ce résultat est donc
satisfaisant.
2.2 Fonctionnement en mode commun
De même nous voulons trouver le gain en mode commun en vue de le comparer au résultat
théorique (même mode opératoire qu’en 1.3).
Dans ce mode Ve1=Ve2 (tensions sinusoïdales de fréquence 100 Hz, d’amplitudes 0.4V).
3
3
1
21 10*75,4
4,010*9,1 
e
SS
mc VVV
A
Aux incertitudes de mesures près, ce résultat correspond à la valeur théorique.
Nous pouvons donc en déduire le taux de réjection en mode commun
1000
mc
d
A
A
TRMC
soit en décibel
dBTRMCdBTRMC 60)log(*20)( 
Nous pouvons conclure que contrairement à la polarisation par résistance, la polarisation par
source de courant permet de limiter le gain en mode commun engendrant un TRMC plus
grand et par conséquent un gain différentiel plus important.
2.2 Caractéristiques de transfert fort signal
a. Nous voulons visualiser les caractéristiques de transfert
)( 11 eS VfV 
et
)( 22 eS VfV 
dans
le cas d’un mode de fonctionnement différentiel.(
21 ee VV 
)
Nous utilisons pour cela le mode XY de l’oscilloscope.