Acoustique musicale

15/04/2017 582664111 1/3
Spécialité Physique
ACOUSTIQUE MUSICALE
Chap.4
 Le son est une onde longitudinale de compression –dilatation des molécules de l’air sans transport de matière.
 La variation de pression due à l’onde sonore est appelée la pression acoustique.
 Les récepteurs sonores (oreille, microphone) sont sensibles aux variations de pression de l’air donc à la pression
acoustique.
I. Intensité sonore et niveau sonore
1. Intensité sonore
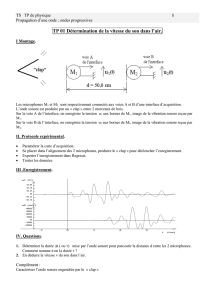
 Expérience :
 On fait varier le « niveau » (LEVEL) de la tension fournie par le
G.B.F.
1.1. Qu’observe-t-on ?
1.2. Quelle est la grandeur caractéristique de la vibration sonore qui varie quand le son devient « plus fort » ?
 Interprétation :
 La puissance sonore P totale émise est proportionnelle au carré de l’amplitude de l’onde sonore. Elle se
répartit sur une portion de sphère dont la surface augmente avec l’éloignement de la source sonore.
 L’intensité sonore I (puissance reçue pour une même unité de surface) s’affaiblit donc quand on éloigne
cette surface réceptrice de la source. C’est le phénomène de dilution du son.
 La puissance sonore reçue par le microphone ( ou l’oreille) est fonction de deux facteurs :
 l’intensité sonore à l’endroit où se situe le récepteur
 la surface du récepteur
 Quand l’intensité sonore est uniforme sur toute la surface du récepteur, la puissance reçue s’écrit :
Preçue = I . Srécepteur avec P en ............ , I en ............ et S en ............
2. Sensibilité de l’oreille humaine
 Expérience :
 On fait varier la fréquence du G.B.F. Recherchez la
zone de fréquence sur laquelle vous entendez.
 Interprétation :
 Le domaine des fréquences audibles par l’oreille
humaine va de 20 Hz à 20 000 Hz
 Remarque : le seuil d’audibilité varie suivant les
individus et leur âge.
3. Niveau sonore
 Expérimentalement on constate que la sensation auditive
n’est pas proportionnelle à l’intensité sonore (deux
musiciens jouant ensemble ne font pas deux fois plus de
bruit qu’un seul).
 Si on multiplie l’amplitude de l’onde sonore par 1,4 ( 2), la puissance émise donc l’intensité sonore est
doublée ( 1,42  2) : la variation de la sensation auditive est faible.
 Pour qualifier la sensation sonore on utilise une grandeur L appelée niveau sonore :
L = 10  log(I
I0) où I0 est l’intensité sonore de référence elle correspond à celle du seuil minimum d’audibilité
moyenne de l’oreille humaine : I0 = 10-12 W.m -2 et I, intensité sonore du son émis allant dans le domaine
audible de 10-12 à 25 W. m -2 (seuil de douleur) ; L s’exprime en décibels (dB) et se mesure avec un sonomètre.
 Application :
3.1. Quand I = I0 , L = …………………………….
3.2. De combien augmente le niveau sonore lorsque l’intensité est multipliée par 10 ? ............
3.3. De combien augmente le niveau sonore lorsque l’intensité est multipliée par 100 ? ............
G.B.F.
haut-parleur (H.P.)
microphone
oscilloscope
G.B.F.
haut-parleur (H.P.)

15/04/2017 582664111 2/3
 La valeur de 90 dB est considérée comme le seuil de danger. Une exposition prolongée à des niveaux sonores
supérieurs entraîne des dégradations irréversibles de l’audition
II. Les sons musicaux
1. Les caractéristiques d’un son musical
 L’intensité d’un son est directement liée à l’amplitude de l’onde.
 La hauteur d’un son dépend de la fréquence de la vibration sonore. Plus la fréquence est élevée, plus le son est
aigu. Plus la fréquence est faible, plus le son est grave.
 Le timbre permet de différencier deux instruments émettant tous les deux un son de même hauteur (même
fréquence) mais qui sera perçu différemment.
2. Exemples
 En utilisant un instrument de musique ( flûte, ), on enregistre trois notes à l’aide du logiciel Audacity puis
on les exploite à l’aide de Regressi. On détermine la période T puis la fréquence f de chacune des notes.
2.1. Comment varient la période et la fréquence lorsque les notes deviennent plus aiguës ? plus graves ?
 On enregistre le son donné par un diapason « La3 » . Cette note est utilisée par les musiciens pour accorder leur
instrument
2.2. Mesurer la fréquence de cette note.
2.3. Sachant que les fréquences d’un La joué sur deux octaves voisines sont pour le La4 : 880 Hz , La2 : 220 Hz,
conclure.
 On enregistre le La3 du diapason, de la flûte et ................................................ .
2.4. Comparer l’allure des courbes et conclure.
3. Analyse d’un son
 La vibration d’une corde ou d’une colonne d’air est la superposition de son mode fondamental et de ses
harmoniques.
 Cette superposition des modes de vibration produit une vibration périodique complexe dont la fréquence est
égale à celle du mode fondamental.
 La réciproque est également vraie et donne lieu au Théorème de Fourier :
Toute fonction périodique de fréquence f peut-être décomposée en une somme de fonctions sinusoïdales de
fréquences f , 2 f, 3 f, ………., k f ( k entier) où
f est appelé le fondamental ou premier harmonique
2 f, 3 f, …….,k f sont appelés les harmoniques de rang 2, 3, ….., k
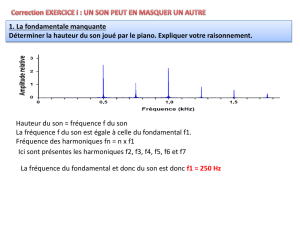
 On peut alors étudier le spectre de Fourier de tout son, en décomposant ce son en tous ses harmoniques. Cela
donne un diagramme en bâton où l’on repère le fondamental et les différents harmoniques, ainsi que leurs
amplitudes relatives.

15/04/2017 582664111 3/3
 La fréquence et l’amplitude de chaque harmonique contribuent au timbre d’un son musical
 La hauteur d’un son est mesurée par la fréquence du fondamental.
 L’enveloppe d’un son ne conserve pas la même amplitude pendant la durée de l’émission car le son évolue dans
le temps. On distingue différentes phases : l'attaque, la libération, le corps (ou sustain) et l'extinction.
3.1. Faire apparaître le spectre de chacun des sons enregistrés, les comparer et conclure
4. Synthèse d’un son
 On utilise l'animation Java : http://pagesperso-orange.fr/gilbert.gastebois/java/fourier/fourier1/fourier1.html
 On superpose les fonctions : Y1 = a1 sin(2 f1 t ) ; Y2 = a2sin (2 (2f1) t ) ; Y3 = a3 sin(2 (3f1) t ) ; etc…. puis
on visualise la courbe Y = Y1 + Y2 + Y3 + …
 Signal créneau : somme des fonctions sinusoïdales suivantes :
Y1 avec a1 = 100 et f1 = 1 f où f est la fréquence du fondamental. Y3 avec a3 = 33 et f3 = 3 f ;
Y5 avec a5 = 20 et f5 = 5 f ; Y7 avec a7 = 14 et f7 = 7 f ; Y9 avec a9 = 11 et f9 = 9 f
III. Les gammes musicales
1. Intervalle de fréquences
 On considère deux sons de fréquences f1 et f2. L’intervalle musical de deux sons est le rapport de leurs
fréquences. Les musiciens ont donné un nom particulier à des rapports de leurs fréquences :
 f2
f1 = 2 pour l’octave ; f2 f1 = 3 2 pour la quinte ; f2 f1 = 5 4 pour la tierce
 Cependant, l’unité légale d’intervalle de fréquence est le savart, défini par : I = 1000 log (f2
f1). Ainsi pour une
octave, le rapport des fréquences est de 2 et donc l’intervalle en savarts vaut : I = 1000 log2 = 300 savarts
2. Gamme tempérée
 La gamme utilisée en occident de nos jours est la gamme tempérée.
 Elle est divisée en 12 intervalles ou degrés chromatiques appelés demi-ton, et séparé par 25 savarts.
 Une gamme contient 7 notes ou degrés diatoniques.
2.1. Démontrer que le rapport r entre deux demi-tons successifs est 12 2.
 Pour un ton on multiplie par 62.
3. Autres gammes
 La gamme de Pythagore a été utilisée de l'antiquité jusqu'au 16ème siècle et, contrairement à ce que laisse
penser son nom, elle n'a pas été créée par Pythagore mais par ses disciples. Pour plus de renseignements, allez
sur la page suivante : http://www.crdp.ac-grenoble.fr/imel/jlj/son_et_lumiere/son/pythagore.htm
 La gamme de Zarlino : voir : http://www.crdp.ac-grenoble.fr/imel/jlj/son_et_lumiere/son/zarlino.htm
 Dans la musique arabe, indienne et chinoise, on utilise d’autres gammes. Voir :
http://www.crdp.ac-grenoble.fr/imel/jlj/son_et_lumiere/son/monde.htm