Correction - NTE Lyon 1

Cliquer sur « affichage » puis « plein écran »
1
Exercices de Résolution des réseaux électriques
1 - Applications des théorèmes de Thévenin et de Norton
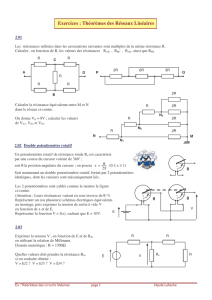
a) Potentiomètre à vide et en charge.
Eléments de Thévenin :
A et B ne sont pas reliés : On reconnaît un diviseur de tension.
)x1(Rx
)x1(RRx )x1(R.Rx
r
xEE
)x1(RRx Rx
U0
Eléments de Norton :
A et B sont reliés par un fil sans résistance. On calcule alors le courant de court-
circuit.
)x1(R E
I0
La résistance du modèle équivalent de Norton est la même que celle du modèle
de Thévenin.
Potentiomètre en charge
Le potentiomètre débite sur une charge résistve Ru .
On remplace le potentionmètre par son modèle équivalent de Thévenin, afin de
déterminer le courant I, par la simple loi de Pouillet.
Loi de Pouillet
A
B
E
R(1-x)
Rx
A
B
E
R(1-x)
Rx

Cliquer sur « affichage » puis « plein écran »
2
Dans un circuit à une maille, le courant est le quotient de la somme
algébrique des f..e.m. et de la somme des résistances
u
R)x1(Rx Ex
I
Si R est faible devant Ru. La simple variation de x, règle la valeur de I. Il faut alors
remarquer que le potentiomètre a une forte consommation “interne”.
b) Passage du modèle de Thévenin au modèle de Norton – Adaptation de
puissance
Le modèle équivalent de Thévenin d’un générateur est donné par une tension à
vide ou f.e.m. E=20V et une résistance r=10.
a) Obtenir par calcul, le courant de court-circuit
A2
10
20
r
E
I0
b) En déduire le modèle de Norton associé
Un générateur de courant parfait de courant 2A en parallèle avec une résistance
de 10Ω, ou une conductance de 0,1S.
c) On branche une résistance R de valeur inconnue sur le générateur.
Exprimer littéralement la puissance dissipée dans R en fonction de E,r et R. Pour
quelle valeur de R, la puissance est-elle maximale ?
Soit U, la tension aux bornes de la résistance R.
E
rRR
U
La puissance consommée par R est donnée par :
2
22
2
2
)Rr( RE
R
E
]
rRR
[
R
U
P
E
R(1-x)
Rx
Charge
Ru
Ru
)x1(Rxr
E.x

Cliquer sur « affichage » puis « plein écran »
3
La dérivée de la fonction
)R(P
par rapport à R a pour 0, la valeur R=r.
Dans ces conditions la puissance est maximale, la charge R est adaptée à la
source de résistance interne r.
2 – Applications du théorème de Millman
G est un générateur dont la f.e.m. E décroît avec le temps de 6,4V à 5,5V en 24h
selon une loi linéaire.
Sa résistance interne est constante et vaut r=5. La charge du montage est
S=10.
En tampon, on place une batterie B de fem constante e=4V et de résistance
interne r’= 0,1.
a) Exprimer la loi de variation de l’intensité dans la charge à l’instant initial
et au bout de 24h.
b) Quelle serait la valeur du courant dans la charge au bout de 24h sans
la batterie ?
c) Quel est le rôle de la batterie
E varie selon la loi
joursent;t9,04,6E 
.
'r
1
S
1
r
1'r
e
r
E
S
1
S
u
i
'r
1
S
1
r
1'r
e
r
E
u
t002,04,0i 
La variation relative de i sur 1 jour est de 0,5%
Sans batterie, la loi de variation de i est
t06,0t43,0i 
La variation relative de i sur 1 jour est de 14%
S
Générateur
Batterie
r
r’
I
i
u
E
e

Cliquer sur « affichage » puis « plein écran »
4
Le rôle de la batterie est de suppléer au déficit de courant du à l’affaiblissement de
E. D’où le nom de batterie tampon.
3 – Applications des méthodes de Kirchoff
On désire trouver les intensités des courants dans toutes les résistances du circuit
suivant. Il s’agit d’un exemple à caractère didactique seulement.
a) Préliminaire
 Combien le réseau a-t-il de nœuds de courant, de branches et de mailles?
2 nœuds A et B ainsi que 3 mailles E1,R1,R – E2,R2,R – E1,R1,R2,E2.
3 branches E1,R1 – R - R2,E2
Il y a trois intensités à trouver donc 3 équations indépendantes. On prend deux
équations de mailles et une de nœud.
 Représenter par une flèche la tension UAB ()
 Représenter par une flèche les courants dans les résistances () en
représentant les deux générateurs en convention générateur et R en
récepteur
Au vu de ces données, il n’y a aucune ambiguïté sur les sens des courants et leur
signe.
On peut aussi représenter les tensions aux bornes des résistances. ().
On désire calculer les trois courants de branches et la tension UAB .
b) Calculer par les lois de Kirchoff
E1=10V
E2= 40V
R1=5
R2=10
R=10
A
B
E1
E2
R1
R2
R
A
B
I1
I2
I

Cliquer sur « affichage » puis « plein écran »
5
Loi de nœud :
21 III 
Lois de mailles : On doit écrire deux équations indépendantes, choisir deux
mailles et écrire l’équation en suivant la maille dans un sens choisi.
0IRRIE0IRRIE
222
111 
Soit à résoudre le système linéaire :
222
111
21
ERIIR0 ERI0IR 0III
)RRRRRR(RE)RR(E
RR0 R0R 111 RRE R0E 110
I2112
221
2
1
22
1
1
)RRRRRR(ER)EE(R
RR0 R0R 111 RE0 RER 101
I2112
2121
2
1
2
11
2
)RRRRRR(RERE
RR0 R0R 111 ER0 E0R 011
I2112
1221
2
1
22
11
E1
E2
R1I1
R2I2
RI
A
B
I1
I2
I