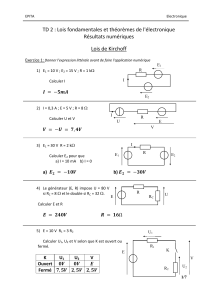
Théorèmes de Norton et Thévenin

TD N° 6 Théorèmes de Norton et Thévenin
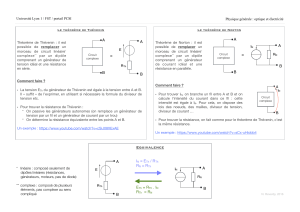
I- Déterminer le générateur de Thévenin équivalent aux deux générateurs de tension (E
1
, R
1
)
et (E
2
, R
2
) montés en parallèle et alimentant la charge R
L
.
E 1
R
2
R
L
R
1
E 2
- En déduire le courant circulant dans la charge,
- Calculer la puissance dissipée par effet joule dans R
L
.
- L’adaptation entre générateurs et charge est elle réalisée.
- Sinon quelle est la valeur de R
L
qui réalise l’adaptation en puissance. Calculer dans ce cas
la puissance maximale transmise.
II- Déterminer le générateur de Norton équivalent au circuit alimentant la résistance R
4
R
2
R
1
R
3
R
4
I
En déduire le générateur de Thévenin équivalent .
Calculer le courant dans la résistance R
4
.
III- On considère le circuit suivant
L
v
R
A
X
R 2
R 1
B
E
1
=1V
E
2
=2V
R
1
=1Ω
R
2
=2Ω
R
L
=2Ω
I=1A
R
1
=1Ω, R
2
=3Ω, R
3
=4Ω
R
4
=2Ω
)sin()(
0
tVtv ω=
V
0
= 3.16 V, ω = 10
5
rd/s, R
1
=1Ω, R
2
=2Ω, L= 40 µH,
La charge connectée entre les points A et B comporte
une résistance R et une réactance X variables.

1- Déterminer les expressions littérales complexes des éléments du générateur de Thévenin
équivalent au circuit alimentant la charge ( R,X).
2- Calculer les valeurs numériques complexes des éléments du générateur de Thévenin.
3- Déterminer les valeurs de R et x pour lesquelles la puissance transmise à la charge est
maximale. En déduire la nature de cette charge.
4- Calculer la puissance maximale fournie à la charge.
IV- Soit le circuit suivant en régime sinusoïdal.
A
eR2
R1i
YAB
B
C
- Déterminer le générateur de courant équivalent au circuit qui alimente le dipôle AB.
- Quelle est l’admittance Y
AB
du dipôle pour laquelle il y aura transfert maximum de
puissance. Définir sa nature. Calculer cette puissance maximale.
V- On considère le circuit ci-dessous où e(t) est une f.e.m sinusoïdale et r est la résistance
interne du générateur.
e(t) R
2
A
C
r
M
v(t)
R 1
Soient
−
e et
−
v les grandeurs complexes associées à e(t) et v(t).
1- Déterminer l’expression littérale de
−
v en appliquant le diviseur de tension puis le
théorème de Thévenin et enfin le théorème de Millman.
2- Calculer l’expression numérique de
−
v et en déduire l’expression numérique de v(t),
3- Déterminer les courants dans chaque branche.
4- Calculer la puissance active dans le dipôle AM alimenté par le générateur (e,r).
)cos(1.0)(
)cos(2)(
tti
tte ω=
ω
=
f=1000Hz
R
1
=R
2
=10 Ω , C=10
µ F
)cos()(
0
tEte ω=
E
0
= 10 V, ω = 1.12 10
5
rd/s, r =1 Ω , R
1
=4 Ω ,
R
2
=5 Ω , C= 5 µ F,