2) Le champ des vecteurs vitesses

CINEMATIQUE
DR 1
COURS
Cinématique graphique
Nom prénom :
Classe :
1) Trajectoires d’un point d’un solide :
1) Enoncé de la trajectoire d’un mobile :
La trajectoire décrite par un mobile est constituée par l’ensemble des positions qu’il occupe au
cours du temps.
2) Définition de la trajectoire d’un point appartenant a un solide :
La trajectoire d'un point mobile est l'ensemble des positions occupées par ce point au cours du
mouvement.
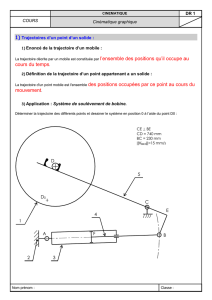
3) Application : Système de soulèvement de bobine.
Déterminer la trajectoire des différents points et dessiner le système en position 0 à l’aide du point D0 :
D0
D1
D
A
B
E
C
F
Echelle  1:6
Echelle des vitesses : 1mm  0,25 mm/s
1
2
3
4
5
CE  BE
CD = 740 mm
BC = 230 mm
||VB4/3||=15 mm/s

CINEMATIQUE
DR 2
COURS
Cinématique graphique
Nom prénom :
Classe :
2) Le champ des vecteurs vitesses :
1) Enoncé
Lorsqu’un solide S1 est en rotation autour d’un
point A fixe dans R0 :
00/1 RSAV
 La connaissance d’un vecteur vitesse
permet de connaître tous les autres par la
construction ci-dessous.
On peut appliquer la formule
wRV RSM 
0/1
avec :
0/1 RSM
V
=norme du vecteur
vitesse en M
R : rayon (ou longueur AM)
W : vitesse de rotation de S1
par rapport à R0 (en rad/s)
2) Application
Déterminer le vecteur vitesse au point B du bout de la pale par rapport au bâti de l’hélicoptère.
0X
0Y
M
0/1 RSM
V
A
0X
0Y
M
0/1 RSMV
A
B

CINEMATIQUE
DR 3
COURS
Cinématique graphique
Nom prénom :
Classe :
3) Equiprojectivité des vecteurs vitesses
1) Enoncé
Soient deux points A et B appartenant à un même solide S et
V(AS/R)
et
V(BS/R)
les vecteurs vitesses des points A et B,
appartenant à S, par rapport à un même référentiel R.
La projection orthogonale de
V(AS/R)
sur
AB
est
égale à la projection orthogonale de
V(BS/R)
sur
AB
.
Concrètement :
AH BK
AHBK
V(AS/R)
V(BS/R)
S
O
x
y
z
Repère R
2) Exploitation du théorème de l’équiprojectivité des vecteurs vitesses
Pour pouvoir appliquer ce théorème et réaliser les différentes constructions, nous devons connaître une
vitesse intégralement, et connaître, au minimum, le support du vecteur vitesse
que nous souhaitons déterminer.
3) Détermination d’une vitesse par double équiprojectivité
Soient :
V(AS/R)
et
V(BS/R)
deux vitesses connues ;
V(CS/R)
une vitesse de direction, de sens et d’intensité inconnue.
La détermination de
V(CS/R)
est possible par double équiprojectivité à partir des deux vitesses
V(AS/R)
et
V(BS/R)
intégralement connues (direction + sens + intensité).
A
B
C
V(AS/R)
V(BS/R)
V(CS/R) ?
O
x
y
z
Repère R
S
A
B
M
N
S
T
C
V(BS/R)
V(CS/R)
V(AS/R)
S
AM CN
BS CT
Remarque : si C était aligné avec A et B, il aurait fallu déterminer la vitesse
V(DS/R)
d’un point D non aligné avec A
et B.

CINEMATIQUE
DR 4
COURS
Cinématique graphique
Nom prénom :
Classe :
4) Application de l’ équiprojectivité
Question : Déterminer le vecteur vitesse au point B appartenant au piston par rapport au bâti.
A
B
0/RbielleAV

CINEMATIQUE
DR 5
COURS
Cinématique graphique
Nom prénom :
Classe :
4) Centre instantané de rotation
1) Définition
Pour tout solide S en mouvement plan par rapport à un repère R, il existe un point I et un
seul, ayant une vitesse nulle (
V(IS/R) 0
) à l’instant t considéré et appelé centre
instantané de rotation ou CIR.
Le CIR possède les propriétés d’un centre de rotation à l’instant (t) considéré. A l’instant suivant (t’=t+t), il y a de
fortes chances pour que le CIR ait changé de position.
2) Détermination et construction du CIR
En tant que centre de rotation, le CIR est situé à l’intersection des perpendiculaires aux supports des vecteurs
vitesses du solide.
A
B
C
V(AS/R) I
V(BS/R)
V(IS/R) 0
I : Centre instantané de rotation
V(CS/R)
S
O
x
y
z
Repère R
3) Détermination des vecteurs vitesses grâce au CIR
Puisque I est le Centre Instantané de Rotation, nous pouvons en déduire que:
V(AS/R) IA 
S/R
V(BS/R) IB 
S/R
En divisant membre à membre, chaque terme des équations, nous obtenons :
V(AS/R)
V(BS/R)
IA 
S/R
IB 
S/R
IA
IB
Soit Finalement :
V(AS/R) IA
IB V(BS/R)
Grâce à cette relation, nous sommes capable de déterminer la norme d’une des vitesses inconnues.
4) Le CIR et les Mouvements Particuliers
Lorsqu’une pièce subit un mouvement de translation, le CIR est rejeté à « l’infini ». De toute
façon, il n’y pas de quoi s’affoler, car dans une mouvement de translation tous les points ont la même vitesse.
Lorsqu’une pièce subit un mouvement de rotation, le CIR se confond avec le Centre de
Rotation. C’est une évidence, mais cette remarque dépanne souvent…