II. Radioactivité

Exos 2007-08 : IMRT1 – Réactions nucléaires spontanées PAGE 1 sur 2
IMRT1 2007-2008 Exercices : Réactions nucléaires spontanées
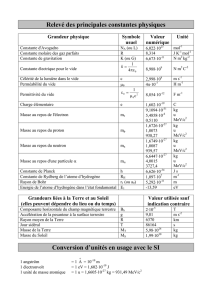
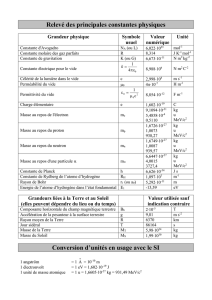
Données numériques pour les exercices :
 Célérité de la lumière dans le vide : C = 3,0.108 m.s-1
 Charge électrique élémentaire : e = 1,6.10-19 C
 Constante de PLANCK : h = 6,62.10-34 J.s
 Unités de masse : 1 u = 1,66054. 10-27 kg = 931,5 MeV.C-2
 Masses des particules : proton – mP = 1,007276 u ; neutron – mN = 1,008665 u ;
particule  –m = 4,0015 u ; électron –me= 5,48.10-4 u ;
noyaux : m(Pu)= 237,9974 u ; m(X) = 233,9899 u ; m(At)= 213,946218 u ;
m(Cs)= 136,8770 u ; m(Ba)= 136,8752 u
Remarque : Quand on utilise la masse atomique ( relative à l'atome ) , il faut
retirer la masse des électrons pour obtenir la masse du noyau (ou du nucléide)
I. Radioactivité
I.1. Plutonium
Le plutonium
238Pu
est radioactif .
1. Écrire l'équation de la réaction de désintégration et identifier le nucléide X
obtenu.
2. Déterminer l'énergie cinétique maximale et la vitesse correspondante de la
particule .
3. On détecte des photons  d'énergie 0,40 MeV. Déterminer l'énergie cinétique
réelle des particules  et la longueur d'onde des photons .
I.2. Astate
L'astate
85
213At
émet une particule  d'énergie 9,080 MeV. Cette émission aboutit
au niveau fondamental du noyau-fils.
1) Écrire la schéma de désintégration de
85
213At
.
2) Calculer la masse du noyau-fils et sa masse atomique.
I.3. Curium
Le curium
242
96Cm
émet des particules  d'énergies différentes, Ec1 = 6,0696 MeV
et Ec2= 6,1129 MeV. La masse du noyau-fils est égale à 237,9974 u.
1) Écrire le schéma de désintégration, sachant que l'une des deux émissions  est
suivie d'une désexcitation  dont on calculera l'énergie.
2) Calculer la masse du noyau de curium 242 et sa masse atomique
3) Calculer la vitesse initiale maximale des particules  émises
4) Déterminer la longueur d’onde du rayonnement  émis

Exos 2007-08 : IMRT1 – Réactions nucléaires spontanées PAGE 2 sur 2
II. Radioactivité
II.1. Phosphore
Le phosphore stable
31
15P
possède deux isotopes radioactifs
30
15P
et
29
15P
. L'un est
émetteur -, l'autre émetteur +. Écrire les réactions de désintégrations en justifiant
chacune d'elles.
II.2. Radioactivité (Extrait ancien B. T. S. 1985 )
Le césium
137
55Cs
est radioactif -. Le nucléide obtenu est le baryum Ba.
1. Écrire l'équation de la réaction de désintégration et déterminer les nombres de
masse et de charge du nucléide obtenu.
2. Calculer en MeV, l'énergie cinétique maximale des particules - émises par des
noyaux de césium au repos.
3. En réalité l'énergie cinétique maximale est de 0,518 MeV et la désintégration
s'accompagne d'un rayonnement  : pourquoi ? Calculer l'énergie des photons  et leur
longueur d'onde.
II.3. Bismuth
Lors de la transformation radioactive
214 214 0
83 84 1
Bi Po e
, un électron émis à un
instant donné a une énergie cinétique initiale de 0,8 MeV. Sachant que l'énergie
maximale des électrons émis au cours de ce processus est 1,15 MeV, quels sont le nom
et l'énergie de la particule associée à cet électron?
II.4. Isobares
La masse de l'atome de carbone 11 est supérieure de 0,002128 u à celle de son
isobare, le bore 11.
1) Quels modes de transformations spontanées peuvent exister de l'un à l'autre ?
2) Calculer, éventuellement, l'énergie maximale des particules émises par le
noyau-père.
3) Répondre aux mêmes questions pour le couple d'isobares lithium 7 et
béryllium 7, la masse du premier étant inférieure de 9,3. 10-4 u à celle du second.
II.5. Positons
Déterminer l'énergie maximale des positons émis au cours de la réaction :
12 12 0
7 6 1
N C e
( masse atomique de l'azote 12 : mN = 12, 018980 u )
III. Familles radioactives
Déterminer le nombre de particules  et - produites dans la suite des
transformations radioactives qui conduisent de
238
92U
à
206
82Pb
et de
232
90Th
( Thorium )
à
206
82Pb
.