Tournez S.V.P.
1
UNIVERSITÉ IBN ZOHR Mercredi 22 mai 2002
FACULTÉ DES SCIENCES Durée : 3H
AGADIR
ÉPREUVE DE PHYSIQUE NUCLÉAIRE
Deuxième partie de la première session
P3
Les 3 problèmes peuvent être traités indépendamment.
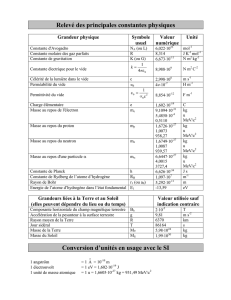
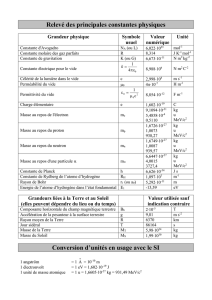
Données pouvant être utiles :
neutron : mn= 939.6 MeV/c2 ; proton : mp= 938.3 MeV/c2 ; électron : me= 0.511 MeV/c2 ;
1u.m.a. = 931.5 MeV/c2 ; c= 3 108 m/s ; Ν = 6.02 1023 ; e = 1.6 10-19 C
137
1
²
;fmMeV197 c
e
c
Problème I
Un faisceau de H+ d’énergie 1 MeV et d’intensité 1 nA est envoyé sur une cible d’or
(
Au
197
79
) très mince de densité
=19.3 g/cm3 et d’épaisseur
= 100 Å.
est l’angle de
diffusion par interaction colombienne des protons sur la cible d’or dans le système centre de
masse.
1- Déterminer la section efficace de diffusion des protons aux angles
90°.
2- Quelle est la probabilité de diffusion d’un proton à un angle
90° ?
3- Combien de protons seront-ils diffusés par seconde à un angle
90° ?
Problème II
Considérons l’interaction colombienne non relativiste d’un projectile de masse M1 et
d’énergie cinétique initiale E0 sur une cible de masse M2 au repos dans le système du
laboratoire. Soient
et
les angles de diffusion du projectile et de la cible par rapport à la
direction d’incidence.
1- Définir le facteur cinématique et le calculer en fonction de
Quelles sont les
valeurs limites de l’angle
que peut avoir le projectile dans sa diffusion ? En déduire
l’énergie cinétique du projectile en fonction de son angle de diffusion ?
2- Déterminer l’énergie de recul de la cible en fonction de son angle de diffusion.
3- Montrer que la loi de transformation entre les angles solides du système centre de
masse et du système du labo est donnée par :
Θγ
Θ)γγ cos1 cos2²1(
d
d
3/2 avec
=M1/M2 et
l’angle de diffusion du projectile dans le SCM, lié à
par les relations :
sin)(sin
et
Θ
Θgg sin
cotcot
.
Tournez S.V.P.
2
Problème III
On envoie un faisceau de particules d’énergie 2 MeV et d’intensité 0.01
A sur une
cible mince de carbone (A=12, Z=6,
=1.65 g/cm3, I = 77.3 eV) d’épaisseur
=8 000 Å.
L’impact du faisceau sur la cible est ponctuel. Un détecteur de surface utile 0.5 cm2 est placé
à 10 cm de l’impact d’interaction et à 120° de la direction du faisceau incident. Ce détecteur
permet d’enregistrer les rétrodiffusées à 120°.
1- Quelle est la vitesse initiale des (en m/s) ?
2- Calculer en MeV/cm puis en keV/
m, la perte d’énergie par unité de parcours S0 de
ces projectiles, à partir de la formule de Bethe simplifiée.
3- En supposant que la perte d’énergie est constante, donc indépendante de l’énergie,
prévoir le spectre en énergie enregistré par le détecteur. Commentaires ?
Afin de déterminer le nombre de particules diffusé dans le détecteur, nous
supposerons, dans la suite du problème, que leur perte d’énergie dans la cible est négligeable.
4- Calculer pour cela le flux du faisceau tombant sue 1 cm2 de la surface de la cible.
5- A Quel angle
du système centre de masse seront diffusées les particules ?
6- Déterminer alors le nombre de particules diffusées par seconde dans le détecteur.
7- Quelle seraient dans ces conditions l’angle de diffusion et l’énergie de recul d’un
noyau de carbone supposé libre ?
1
/
2
100%
