I- Système triphasé

FCMN 10 mai 2005
PhG-Physique
I- Système triphasé
On considère les systèmes triphasés de tensions (réseau de distribution) et les systèmes
triphasés de courants.
Trois grandeurs sinusoïdales, de même fréquence, forment un système triphasé si elles
sont déphasées les unes des autres de
Error!
ou 120°.
Un système triphasé est équilibré lorsqu'il est formé de trois grandeurs ayant la même
valeur efficace.
Exemple : système triphasé direct équilibré de tensions
u1 = U 2 cos  t
u2 = U 2 cos
Error!
u3 = U 2 cos
Error!
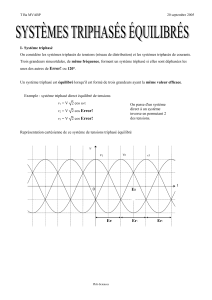
Représentation cartésienne de ce système de tensions triphasé équilibré
II-
Installation triphasé
Pour utiliser un système triphasé de tensions ou de courants, il faut une installation triphasée.
1- Une source
La source est formée de trois générateurs qui
délivrent une f.é.m de même valeur efficace.
L'ensemble représente le principe d'un
alternateur triphasé.
Exemple : e1 = E 2 cos  t
e2 = E 2 cos
Error!
e3 = E 2 cos
Error!
2- Une charge
C'est un récepteur formé de trois impédances
identiques pour un régime équilibré.
On passe d'un
système direct à un
système inverse en
permutant 2 des
tensions.
0
u
u1
u2
u3
Error!
Error!
Error!
Error!
t
Z
Z
Z
e1
e2
e1
N'N
SOURCE CHARGE
i1
i3
i2

Error!
Error!
Error!
1
V
12
U
31
U
23
U
3
V- 
2
V
2
V
3
V
1
V
1
V
3- Une ligne
Elle comporte trois fils appelés « phases ». En régime équilibré, ces trois fils sont
parcourus par des courants d'intensités i1, i2 et i3 de même valeur efficace, déphasées d'un
angle  par rapport aux f.é.m respectives e1, e2 et e3.
i1 = I 2 cos ( t – )
i2 = I 2 cos
Error!
i3 = I 2 cos
Error!
Un quatrième fil, le neutre, relie les points N et N'.
Il peut être supprimé dans certains cas (ligne haute tension par exemple).
III- Tensions simples – Tensions composées
1- Définitions
Les tensions simples v1, v2 et v3 sont mesurées entre chaque phase et le neutre.
En régime équilibré les tensions simples ont même valeur efficace :
V1 = V2 = V3 = V
Les tensions composées u12, u23 et u31 sont les différences de potentiel entre deux phases.
u12 = v1 – v2 u23 = v2 – v3 u31 = v3 – v1
En régime équilibré les tensions composées ont même valeur efficace :
U12 = U23 = U31 = U
2- Représentation de Fresnel
À chaque tension sinusoïdale, on associe un
vecteur de Fresnel.
Les trois tensions simples donne la figure ci- contre
Le sens trigonométrique est le sens positif.
Construisons le diagramme de Fresnel des
tensions composées à partir de celui des
tensions simples.
2112 VVU 
3223 VVU 
i2
i1
iN
i3
u31
v3
u23
u12
v2
v1
2
3
1
N
0
–
Error!
–
Error!
2
V
3
V
1
V
+

FCMN 10 mai 2005
PhG-Physique
3
I
2
I
2
I
3
I
1
I
1331 VVU 
Par exemple, le vecteur
3223 VVU 
est obtenu par l'addition des vecteurs
2
V
et
3
V
.
Les déphasages entre les tensions u12 et v1, u23 et v2, u31 et v3 sont égaux.
Le système des tensions composées est en avance de
Error!
rad sur celui des tensions
simples.
3- Relation entre U et V
La construction des vecteurs de Fresnel des tensions composées
fait apparaître des triangles isocèles.
Pour le triangle isocèle OMA :
OA = 2 OH et OH = OM cos
Error!
soit : U = 2 V cos
Error!
avec cos
Error!
=
Error!
On obtient : U = V 3
IV- Couplages
1- Couplage en étoile (montage en étoile)
Les éléments d'un récepteur ou d'un générateur sont couplés comme l'indiquent la
figure.
Chaque élément est traversé par le courant qui
parcourt la ligne à laquelle il est relié.
La tension aux bornes d'un élément est la tension
simple, soit : V =
Error!
Pour un montage équilibré, les courants en ligne ont
la même valeur efficace : I1 = I2 = I3.
La loi des nœuds au point N donne : i1 + i2 + i3 = 0
En régime équilibré, le courant dans le neutre est nul.
Le fil de neutre joue le rôle de protection si, par
exemple, une des phases est coupée.
A
M
H
Error!
O
Error!
23
U
3
V- 
2
V
u12
i1
i2
i3
1
2
3
u23
v2v3
v1

u12
i1
i2
i3
1
2
3
u23
j1
j2
j3
1
J- 
2
J
3
J- 
1
J
2
J- 
3
I
2
I
3
J
3
I
1
I
2- Couplage en triangle
Les éléments d'un récepteur ou d'un générateur
sont couplés comme l'indiquent la figure.
Ces éléments sont soumis à la tension composée
de valeur efficace U.
Le courant qui les traverse n'est pas le courant
en ligne.
En appliquant la loi des nœuds on écrit :
i1 = j1 – j3
i2 = j2 – j1
i3 = j3 – j2
La représentation de Fresnel des courants traduit graphiquement les relations vectorielles à
ces égalités.
Le système des intensités en ligne est en
retard de
Error!
rad sur le système des
intensités traversant chaque branche.
On obtient une relation analogue à celle des
tensions pour les valeurs efficaces des
intensités des courants :
I = J 3