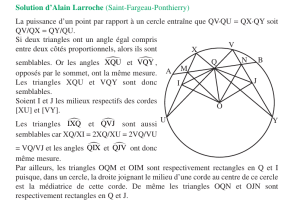
Le Théorème des angles inscrits

Page 1 sur 4
Illustration :
Le Théorème des angles inscrits
I/ Introduction
On apprend en 4ème le théorème suivant :
Soit un cercle de centre O.
Si AMB est un triangle inscrit dans ce cercle
et qu’il possède un côté qui est un diamètre de ce cercle
Alors AMC est un triangle rectangle.
Remarque : La réciproque est vraie
On a donc 
=90° et  =180° .
On observe que 
 est la moitié de 
Existe–t-il une généralisation de cette observation ? la réponse est oui
II/Vocabulaire : Angles inscrits, angles au centre
1°) Angles au centre
Dans un cercle de centre O, un angle au centre est un angle tel que son sommet soit le centre O.
Exemples :
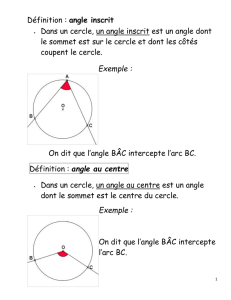
2°) Angles inscrits
Dans un cercle de centre O, un angle inscrit est un angle tel que son sommet
soit un point du cercle et que ses 2 côtés coupent ce cercle.
Exemples :
 est l’angle au centre
qui intercepte l’arc de cercle 
 est l’angle au centre
qui intercepte l’arc de cercle 
 et   sont deux angles
inscrits qui interceptent
le même arc de cercle 

Page 2 sur 4
II/ Enoncé du théorème des angles inscrits
Soit un cercle de centre O.
Soit 
 un angle au centre qui intercepte l’arc de cercle   .
Tous les angles inscrits qui interceptent le même arc 
 mesurent la moitié de angle au centre 
Illustrations
Dans les 2 cas : 
=
A gauche, on a :
,   ont la même mesure

Page 3 sur 4
Preuve :
Cas 1 : O est dans le secteur angulaire 
Cas2 : O est hors du secteur angulaire 
On trace en pointillés le diamètre ayant M pour extrémité on le note [MN]
On trace en pointillés les segments [OA], [OB], [AN] et [NB]
On pose 
x et 
=y
Dans le cas n°1, on a :
 =x+y
Dans le cas n°2, on a : 
 =x-y
Calcul de 
 :
MOA et MOB sont 2 triangles isocèles en O donc
=x et  =y
MAN et MBN sont 2 triangles rectangles en
respectivement A et B donc :
=90-x et  =90-y
Dans un triangle la somme des 3 angles est égale
à 180° donc dans les triangles isocèles OAN et
OBN on a :
= 180-2×(90-x)=2x
=180-2×(90-y)=2y
Calcul de 
 :
MOA et MOB sont 2 triangles isocèles en O donc
=x et  =y
MAN et MBN sont 2 triangles rectangles en
respectivement A et B donc :
=90-x et  =90-y
Dans un triangle la somme des 3 angles est égale
à 180° donc dans les triangles isocèles OAN et
OBN on a :
= 180-2×(90-x)=2x
=180-2×(90-y)=2y
Conclusion du cas n°1 :
 =
=2x+2y
=2(x+y)
= 2
Conclusion du cas n°2 :
 =
=2x-2y
=2(x-y)
= 2

Page 4 sur 4
III/Propriété des angles inscrits interceptant un petit arc 
 et un grand arc 
Propriété :
Soit 
 un angle inscrit interceptant le petit arc de cercle   (en rouge)
et 
 un angle inscrit interceptant le grand arc de cercle   (en vert)
Les angles 
 et   sont supplémentaires (leur somme est égale à 180°)
Preuve :
Soit D’ le symétrique de D par rapport à O.[DD’] est un diamètre donc
DAD’ et DBD’ sont deux triangles rectangles en respectivement A et B.
Dans le quadrilatère DAD’B la somme des 4 angles est égale à 360°.
Donc 
 + 
 =180 c'est-à-dire : 
 et 
 sont supplémentaires
 et 
 sont des angles inscrits qui interceptent le même petit arc de cercle 
donc 
 = 
 . Conclusion : 
 et   sont supplémentaires