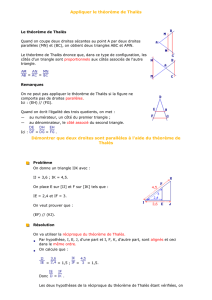
Théorème de Thalès

Théorème de Thalès.
Applications à la géométrie du plan et de l’espace
Le théorème de Thalès fait partie des théorèmes que l’on rencontre pour la première
fois au Collège. Tout d’abord sous la forme du théorème des milieux, puis dans la
configuration d'un triangle coupé par une droite parallèle à l'un des côtés.
Pré requis :
-Aire d’un triangle.
- Droite orientée.
- Mesure algébrique.
- Application affine et application linéaire associée.
- Calcul vectoriel.
Cadre :
On se placera dans le plan P et l’espace E en tant qu’espaces affines euclidiens, en notant
P
ur
et
E
ur
leurs espaces vectoriels associés.
Plan :
I- Configuration triangulaire de Thalès.
II- Théorème de Thalès dans le plan.
III- Théorème de Thalès dans l’espace.
IV- Projections dans le plan et l’espace.
V- Théorème de Ménélaüs.
Démonstrations proposées :
- Théorème de Thalès dans le plan.
-Théorème de Ménélaüs.
Rappel :
Axiome de Pasch :
Étant donné trois points A, B, C, non alignés, si une droite D ne passant par aucun des
sommets du triangle ABC, rencontre l'un des segments ]AB[, ]BC[, ]CA[, alors elle en
rencontre un autre.

I- Configuration Triangulaire de Thalès.
Théorème 1 :
Soient ∆1 et ∆2 deux droites strictement parallèles du plan P, et soient D et D’ deux
droites sécantes en O, non parallèles à
1
∆
, qui coupent respectivement les droites ∆1 et ∆2 en
A, B et A’, B’. On a alors
'
'
OB OB
OA OA
= ; O,A,B et O, A', B' sont dans le même ordre.
Preuve :
1) On veut montrer que O, A, B sur D et O, A’, B’ sur D' sont dans le même ordre. Pour cela
supposons que le point A appartienne à ]OB[.
Alors,
1
∆
coupe ]OB[, comme
1
∆
ne passe pas par O – elle serait alors confondue avec D – et
ne passe pas par B' – elle couperait
2
∆
– l’axiome de Pasch assure alors qu’elle coupe ]BB’[
ou ]B’O[.
Supposons qu’elle coupe ]BB’[ en M.
Alors ∆1 ne serait pas strictement parallèle à ∆2, donc ∆1 coupe]OB’[.
Si c'est le point B qui appartient à ]OA[, une démonstration analogue à la précédente point
par point, montre que B' appartient à ]OA'[.
2) On veut monter alors que
'
'
OB OB
OA OA
=
.
En notant hB la hauteur issue de B et hB’ la hauteur issue de B’, on a :
A (OBB′) =
1
2
OB.hB ′ et A (OAB′) =
1
2
OA.hB ’ . D′où
( ')
( ')
OBB OB
OAB OA
=
A
A
.
De même, A (OBB′) =OB′.hB et A (OA′B) =OA’.hB. D’où
( ') '
( ' ) '
OBB OB
OA B OA
=
A
A
.
Montrons alors que A (OAB′)= A (OA′B).
A (OBB′)= A (OAB′) + A (ABB′), car A est entre O et B, et donc ABB’ et OAB’ ont une
intersection réduite au segment [AB’]. De même, A’ étant entre O et B’, on a
A (OBB′)= A (OBA′) + A (A’BB′). On en déduit que A (OAB′)= A (OA′B).
Et donc
'
'
OB OB
OA OA
=
.
Remarque : Le théorème que nous venons d’énoncer est un cas particulier du théorème de
Thalès. Un cas plus général est énoncé ci-après.
II- Théorème de Thalès dans le plan.
Théorème 2 :
Soient D1, D2, et D3 trois droites strictement parallèles, et soient d et d’ deux droites
non parallèles à
1
D
qui coupent respectivement D1, D2, et D3 en A, B, C et en A’, B’, C’.
On a alors :
' '
' '
A C AC
A B AB
=
.

Démonstration :
•Si d est parallèle à d’, le résultat est immédiat puisqu’on obtient deux
parallélogrammes.
• On suppose alors d et d’ sécantes. On note O leur point d’intersection.
On considère l’homothétie h de centre O qui transforme A en B et h’ l’homothétie de centre
O qui transforme A en C.
Alors il existe
α
et
β
appartenant à Ë, tels que :
OB OA α =
uuur uuur
et
OC OA β =
uuur uuur
.
On a alors :
( )
1AC AO OC OA β = + = −
uuur uuur uuur uuur
et
( )
1AB OA α = −
uuur uuur
.
Si
α
= 1,
OB OA =
uuur uuur
et donc D1 = D2 ce qui est impossible.
On peut alors écrire:
1
1
OA AB
α
=−
uuur uuur
d’où
1
1
AC AB
β
α
−
=−
uuur uuur
.
De plus h(A)=B et h′(A′)=K où K est l’intersection de (OA’) et de la parallèle à (AA’)
passant par B.
Donc h(A′)=B′. On a alors
1
1
' ' ' ' A C A B
β
α
−
=−
uuuuur uuuuur
.
Par le même raisonnement, h′(A′)=C.′
De plus A, B et C sont alignés, ainsi que A’,B’ et C’.
En passant aux mesures algébriques, on a :
' '
' '
A C AC
A B AB
=
.
Proposition 3: (Réciproque du théorème de Thalès).
Soient deux droites d et d’ et trois droites D1, D2 et D3 coupant respectivement d et d’
en A, B, C,distincts deux à deux, et A’, B’, C’,distincts deux à deux.
Si D1 est parallèle à D2 et si
' '
' '
A C AC
A B AB
=
, alors D3 est parallèle à D1 et D2.
Démonstration :
Soit
3
' D
la parallèle à D1, passant par C qui coupe d’ en K.
D’après le théorème direct,
' '
'
A B AB
A K AC
=
= et comme par hypothèse,
' '
' '
A C AC
A B AB
=
, alors
' ' ' A K A C =
, et comme A’, K et C’ sont alignés, on a K = C', d’où D3 =
3
' D
, et D3 est
parallèle à D1, et à D2..
III- Théorème de Thalès dans l ’ espace.
Théorème 4 :
Soient
1
P
,
2
P
et
3
P
trois plans strictement parallèles, et D et D’ deux droites non
parallèles à
1
P
.
On note A, B, C, les points d’intersection de D avec
1
P
,
2
P
et
3
P
. On note également A’, B’,
C’ ceux de D’ avec
1
P
,
2
P
et
3
P
. Alors :
' '
' '
A C AC
A B AB
=
.

Démonstration :
Si D et D’ sont coplanaires, on est ramené au cas du théorème de Thalès dans le plan.
On suppose donc D et D’ non coplanaires. On trace la parallèle
1
D
à D’ passant par A.
Elle coupe
2
P
en
1
B
et
3
P
en
1
C
. On est alors ramené au cas plan du théorème de Thalès dans
le plan déterminé par D et D1.
Ainsi,
1
1
AC AC
AB AB
=
.
Dans le plan déterminé par D1 et D’, on obtient
1
1
' '
' '
AC A C
AB A B
=
.
Donc
' '
' '
A C AC
A B AB
=
.
Proposition 5 :
Si trois points A, B et C, d’une droite D et trois points A’, B’ et C’, d’une droite D’
vérifient
' '
' '
A C AC
A B AB
=
, et si D et D’ ne sont pas coplanaires, alors il existe un plan de l’espace
auquel les trois droites (AA’), (BB’) et (CC’) sont parallèles.
Démonstration :
Soit deux droites D et D’ non coplanaires.
On a alors (AA’) non parallèle à (BB’), car sinon le plan défini par les droites (AA’) et (BB’)
contiendrait D et D’.
Soit (Ax) la parallèle à (BB’) passant par A, et (By) la parallèle à (AA’) passant par B.
Le plan
1
P
défini par (AA’) et (Ax), et le plan
2
P
, défini par (BB’) et (By), sont parallèles car
deux sécantes de l’un sont parallèles à deux sécantes de l’autre.
Soit P le plan passant par C parallèle à
1
P
et
2
P
.
Il coupe D’ en K et d’après le théorème de Thalès dans l’espace :
' '
'
A B AB
A K AC
=
.
Or
' '
' '
A C AC
A B AB
=
, donc
' ' ' A K A C =
, et comme A’,C’ et K sont alignés, K = C’.
Les trois droites sont donc bien dans trois plans parallèles.
Remarque :
Cet énoncé ne constitue pas une réciproque du théorème de Thalès dans l’espace.
IV- Projections dans le plan et l ’ espace.
I) Dans le plan.
Rappel :
Dans le plan, étant donné un point M et une droite D’, il existe une seule droite
M
d
passant par M et parallèle à D’. Si D est une droite non parallèle à D’,
M
d
et D sont alors
sécantes en un point m.

Définition 6 :
L’intersection de D avec la droite passant par M et parallèle à D’ est appelée le projeté
de M sur D parallèlement à D’. L’application qui à tout point M du plan associe son projeté m
sur D parallèlement à D’, s’appelle la projection ponctuelle sur D parallèlement à D’.
Proposition 7 : (Traduction du théorème de Thalès en terme de projection)
Soient D et D’ deux droites non parallèles, et A, B et C, trois points du plan.
Si A, B, C sont alignés, il existe un réel λ tel que
AC AB λ =
uuur uuur
, alors les projetés A’, B’, C’ de
A, B, C sur D parallèlement à D’ vérifient également
' ' ' ' A C A B λ =
uuuuur uuuuur
.
Démonstration :
(Utilisation direct du théorème de Thalès).
Proposition 8 :
Les projections conservent les milieux.
Démonstration :
Cas particulier de la proposition 7. Il suffit de prendre λ = 2.
Proposition 9 :
L’image d’un parallélogramme par une projection ponctuelle est un parallélogramme
aplati. (On parle de conservation de l’équipollence).
Démonstration :
Soit ABCD un parallélogramme.