10 Symétrie

Maths 6e10. Symétrie 2012-2013
10 Symétrie
10.1 Axe de symétrie d’une figure
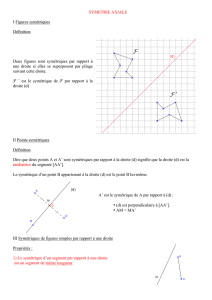
Une droite est un axe de symétrie d’une figure si les deux parties de la figure situées de
part et d’autres de la droite se superposent exactement par pliage suivant cette droite.
Exemples :lesdiagonalesd’unlosangesontsesaxesdesymétrie;labissectrice d’un angle
est son axe de symétrie ; tout diamètre d’un cercle est un de sesaxesdesymétrie.
10.2 Médiatrice d’un segment
A
B
M
P
∆
Le segment [AB]adeuxaxesdesymétrie:ladroite(AB)
elle-même et la droite ∆perpendiculaire à la droite (AB)
passant par le milieu du segment [AB].
Définition :Ladroiteperpendiculaireàunsegmentenson
milieu s’appelle la médiatrice du segment.
Théorèmes :
1. Si un point appartient à la médiatrice d’un segment, alors il est équidistant des ex-
trémités du segment ;
2. Si un point est équidistant des extrémités du segment, alors il appartient à la média-
trice du segment.
fig.1 fig.2a fig.2b
Construction de la médiatrice d’un segment :
–règlegraduéeetéquerre(fig.1 ):mesurerlesegment,divisersamesurepardeux,tracer
le milieu, puis la perpendiculaire à l’aide de l’équerre ;
–compasetrèglenongraduée(fig.2a ou fig.2b):
–aveclecompasontracedeuxarcsdecerclesdemêmerayonetdecentresrespectifsles
extrémités du segment : l’intersection de ces deux arcs est unpointdelamédiatrice,
car il est équidistant des extrémités du segment ;
–demêmeontraceunsecondpointdelamédiatrice(onpeutgarder le même rayon
en traçant un point de l’autre côté du segment) ;
F.Bonomi – 24/32 – prog 2005

Maths 6e10. Symétrie 2012-2013
–lesdeuxpointsconstruitspermettentdetracerlamédiatrice du segment.
Remarque :l’utilisationducompasestplusrapideetplusprécisequela règle graduée et
l’équerre ; de plus il n’est pas nécessaire de tracer le segment pour connaître sa médiatrice ;
on peut également se servir de cette méthode pour construire le milieu du segment en
traçant l’intersection du segment avec la médiatrice.
10.3 Bissectrice d’un angle
La bissectrice d’un angle est aussi son axe de symétrie.
Rappel :labissectriced’unanglepeutêtreconstruitededeuxfaçons (voir chapitre sur
les angles) :
–àl’aided’unrapportenmesurantl’angleet,aprèsdivisiondecettemesurepardeux,
en traçant la droite issue du sommet de l’angle qui partage cetangleendeuxangles
de même mesure.
–àl’aideducompasetdelarèglenongraduéeenconstruisantdeux points équidistants
du sommet de l’angle sur chacun des côtés de l’angle, puis un point équidistant des
deux points ainsi obtenus.
10.4 Axes de symétrie d’un triangle
En général un triangle n’a pas d’axe de symétrie : on parle de triangle quelconque.
Théorèmes :
1. Si un triangle est isocèle, alors il a un axe de symétrie et son axe de symétrie est
àlafoisla bissectrice de l’angle formé par les deux côtés de même longueur et la
médiatrice du côté opposé à ce sommet.
2. Si un triangle a un axe de symétrie, alors il est isocèle.
3. Si un triangle est équilatéral, alors il a trois axes de symétrie qui sont les bissectrices
de ses angles et les médiatrices de ses côtés.
4. Si un triangle a au moins deux axes de symétrie distincts, alors il est équilatéral.
10.5 Axes de symétrie d’un quadrilatère
En général un quadrilatère n’a pas d’axe de symétrie : on parledequadrilatèrequelconque.
Théorèmes :
1. Un trapèze isocèle a un axe de symétrie qui est la médiatricecommunedesesdeux
bases (côtés parallèles).
F.Bonomi – 25/32 – prog 2005

Maths 6e10. Symétrie 2012-2013
2. Un cerf-volant à un axe de symétrie qui est une de ses diagonales.
3. Un rectangle a deux axes de symétrie qui sont les médiatrices de ses côtés.
4. Un losange a deux axes de symétrie qui sont ses diagonales.
5. Un carré a quatre axes de symétrie qui sont les médiatrices de ses côtés et ses
diagonales. (preuve :lecarréestàlafoisunrectangleetunlosange.!)
10.6 Symétrie axiale ou réfléxion
Si deux figures se superposent exactement par pliage suivant une droite, alors on dit
que ces deux figures sont symétriques par rapport à cette droite qui est appelée axe de
symétrie.
On parle de symétrie ou de réflexion par rapport à une droite.
Théorème :deuxfiguressymétriquesparrapportàunedroiteontmêmesdimensions,
mêmes formes et même aire.
Preuve :lesdeuxfiguressontsuperposablesparretournement.!
Construction de la symétrie :
Deux points Met M!sont symétriques par rapport à l’axe ∆si la droite ∆est la média-
trice du segment [MM!].
Pour construire le point M!symétrique du point Mpar rapport à la droite ∆on utilise
le principe de la construction de la médiatrice d’un segment :
M
M!
∆
M
M!
∆
F.Bonomi – 26/32 – prog 2005

Maths 6e10. Symétrie 2012-2013
–aveclaréglegraduéeetl’équerre:tracerlaperpendiculaire à l’axe de symétrie ∆
passant par le point M;surcetteperpendiculairereporterladistancedupointMà
l’intersection de l’axe ∆avec la perpendiculaire de l’autrecôtédel’axe∆;lepoint
obtenu est le symétrique M!de M(l’axe ∆est la médiatrice du segment [MM!]).
–aveclecompasetlarèglenongraduée:tracerunarcdecercledecentreMcoupant
l’axe ∆en deux points; tracer deux arcs de cercle de même rayonetdecentresrespectifs
les deux points tracés sur l’axe ∆; ces deux arcs se coupent en M!,symétriquedeM
par rapport ∆.
10.7 Propriétés et théorèmes
Théorème :lasymétrieaxialeconservelesdistancesetlesangles,donc :
–lesymétriqued’unsegmentestunsegmentdemêmelongueur;
–lesymétriqued’unedroiteestunedroite;
–lesymétriqued’uncercleestuncercledemêmerayon;
–lesymétriqued’unangleestunangledemêmemesure.
Autres résultats intéressants :
–siunpointsetrouvesurl’axedesymétrie,alorsilestsonpropre symétrique ;
–siunsegmentouunedroitecoupel’axedesymétrie,alorslesymétrique de ce segment
ou de cette droite passe par ce point d’intersection avec l’axe.
Exemple :
On construit le symétrique du triangle ABC par rapport au côté [AC](ladroite(∆)est
l’axe de symétrie).
A
C
B
(∆)
B!
Les points Aet Cappartiennent à l’axe
de symétrie donc le point Aest son
propre symétrique, de même pour C.
Il suffit donc de construire le symé-
trique B!de B,alors[AB!]estlesy-
métrique de [AB]et[CB!]estlesy-
métrique de [BC].
La conservation des longueurs par la
symétrie permet d’écrire les égalités :
AB =AB!et CB =CB!.
La conservation des angles par la sy-
métrie permet d’écrire les égalités :
!
BAC =" B!AC,! BCA =" B!CA et ! ABC =" AB!C(l’angle droit reste un angle droit).
F.Bonomi – 27/32 – prog 2005