mots et notions géométriques livretC3

Arden Quin, «
Arden Quin, «Arden Quin, «
Arden Quin, « sans titre
sans titresans titre
sans titre

Page 1 Repérage sur quadrillage ; agrandissement ; réduction.
Page 2 Mesurer avec la règle graduée, l’équerre, le compas.
Page 3 Points, droites et segments - perpendiculaires et parallèles.
Page 5 Angles
Page 6 Tracer une médiatrice - tracer une bissectrice.
Page 7 Symétrie axiale.
Page 8 Parler des polygones
Page 9 Parler des triangles — propriétés des triangles.
Page 10 Construire des triangles.
Page 11 Décrire des quadrilatères.
Page 12 Les propriétés des quadrilatères : tableau de synthèse.
Page 13 Tracer des quadrilatères.
Page 14 Vocabulaire du cercle et du disque.
Page 15 Des solides.
Page 16 Le vocabulaire des solides — les patrons de solides.
Page 17 Suivre un programme de construction — Reproduire une figure.

Le quadrillage est un outil très pratique pour agrandir, réduire, faire de la sy-
métrie. Mais il faut d’abord savoir s’y repérer.
Voici un quadrillage 3x6
Les cases sont repérées par leurs
coordonnées.
Exemple : o est dans (B ; 4)
est dans (C ; 6)
A
B
C
1 2 3 4 5 6
o
Voici un quadrillage 3x6
Les noeuds sont repérés par leurs
coordonnées.
Exemple :
est sur (B ; 5)
est dans (A ; 2)
A
B
1 2 3 4 5
Une réduction
Un agrandissement
1

B
O
1 2 3
3 4 3
5 6 3
7 8 9
0 1 9 10
B
A
8 cm et 6 mm [AB] = 8, 6 cm
Le point A est placé juste en
face du « 0 » de la règle.
On utilise la règle.
3
3 4 3
5 6 3
7 8 9
9 1
la règle est cassée ?
A
B
[AB] = 7, 5 cm - 5 cm = 2, 5 cm
7 cm et 5 mm
Le point A est placé juste en
face d’un nombre entier de la
règle.
5 cm
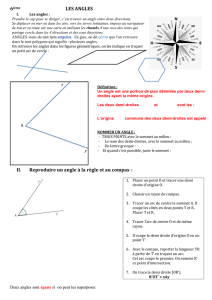
Un angle
droit
Les segments sont
perpendiculaires en O B
B
O O
Un angle
quelconque Un angle
quelconque
Les segments ne sont pas
perpendiculaires en O
A
A
A
L M N
Les segments L et N
ont la même longueur.
2

Le point est ce qui montre la position dans
l’espace. Il est le départ (et l’arrivée !) d’une
construction géométrique. Il faut toujours
le marquer (en général par une petite croix
ou … un point !) et le nommer .
A
Le point A
A
B
Quand on a marqué deux points, on peut tracer une
droite ; une demi-droite : un segment.
Une droite est infinie.
Une demi-droite a une extrémité...mais est quand
même infinie.
Un segment a deux extrémités : on peut le mesurer.
A
B
A
B
La droite (A B) La demi-droite [A B) Le segment [A B]
Lorsque deux droites ne se croisent jamais et que la
distance entre ces deux droites est toujours la
même, les deux droites sont parallèles.
Deux droites parallèles
(AB) // (CD)
A
B
C
D
1,58
1,58
Ici, la distance entre les droites
est de 1,58 cm
2 points sont toujours alignés.
Pour vérifier si trois points (ou plus) sont
alignés, il faut vérifier qu’ils sont sur la
même droite, en utilisant la règle.
A , B et C sont alignés.
D, E et F ne sont pas alignés.
A
B
C
D
E
F
3