2nd Phys6 Cours L`attraction universelle dans notre système solaire
2nd
Phys6
Cours L’attraction universelle dans notre système solaire
I. Loi de gravitation universelle.
La constante universelle de gravitation est G = 6,67.10–11 N.m2.kg–2
Remarque : La relation de Newton n’est correcte que si les corps sont soit homogènes, soit possèdent une répartition
sphérique de leur masse, comme la Terre.
Exemple 1: Calculer la valeur de la force d’attraction gravitationnelle exercée par la Terre sur la Lune, puis celle exercée par la Lune
sur la Terre.
Données :
• masses de la Lune et de la Terre : mL = 7,35.1022 kg, mT = 5,95.1024 kg.
• distance moyenne Terre-Lune : d = 384.103 km.
L’interaction gravitationnelle est toujours attractive et se manifeste de trois façons. La première est la chute verticale
des corps ; c’est le cas par exemple d’un objet qui tombe devant nous. La deuxième est une modification de la trajectoire
des corps ; ce serait le cas d’un astéroïde qui, attiré par notre planète, verrait sa course modifiée (voir exemple p 279).
La troisième est la satellisation, par exemple celle de la Lune autour de la Terre ; de la Terre autour du Soleil… La
trajectoire du satellite peut être circulaire, elliptique ou plus complexe.
Ainsi, toute manifestation de l’interaction gravitationnelle prend l’une de ces trois formes : chute, déviation
ou satellisation.
II. Le poids d’un corps sur Terre.
gT = 9,8 N.kg–1 est l’intensité de la pesanteur à la surface de notre planète.
La valeur P du poids de ce corps peut être assimilée à la valeur F de la force de gravité exercée par la Terre sur ce corps,
ce qui permet d’écrire la relation :
Remarque : La distance entre le centre de gravité du corps et celui de la Terre se confond avec le rayon de la Terre si le
corps est proche du sol. (d=RT)
III. Le poids d’un corps sur la Lune.
Le poids d’un même corps dépend de l’astre sur lequel il se trouve.
Ainsi, pour un corps de masse m à la surface de la Lune (de masse ML et de rayon RL), il est donné par la relation :
L’intensité de la pesanteur à la surface de la Lune prend une valeur environ 6 fois plus faible
que l’intensité de la pesanteur à la surface de la Terre : gL = 1,6 N.kg–1.
Ainsi, le poids d’un corps est environ 6 fois plus faible sur la Lune que sur la Terre, alors que sa masse reste inchangée.
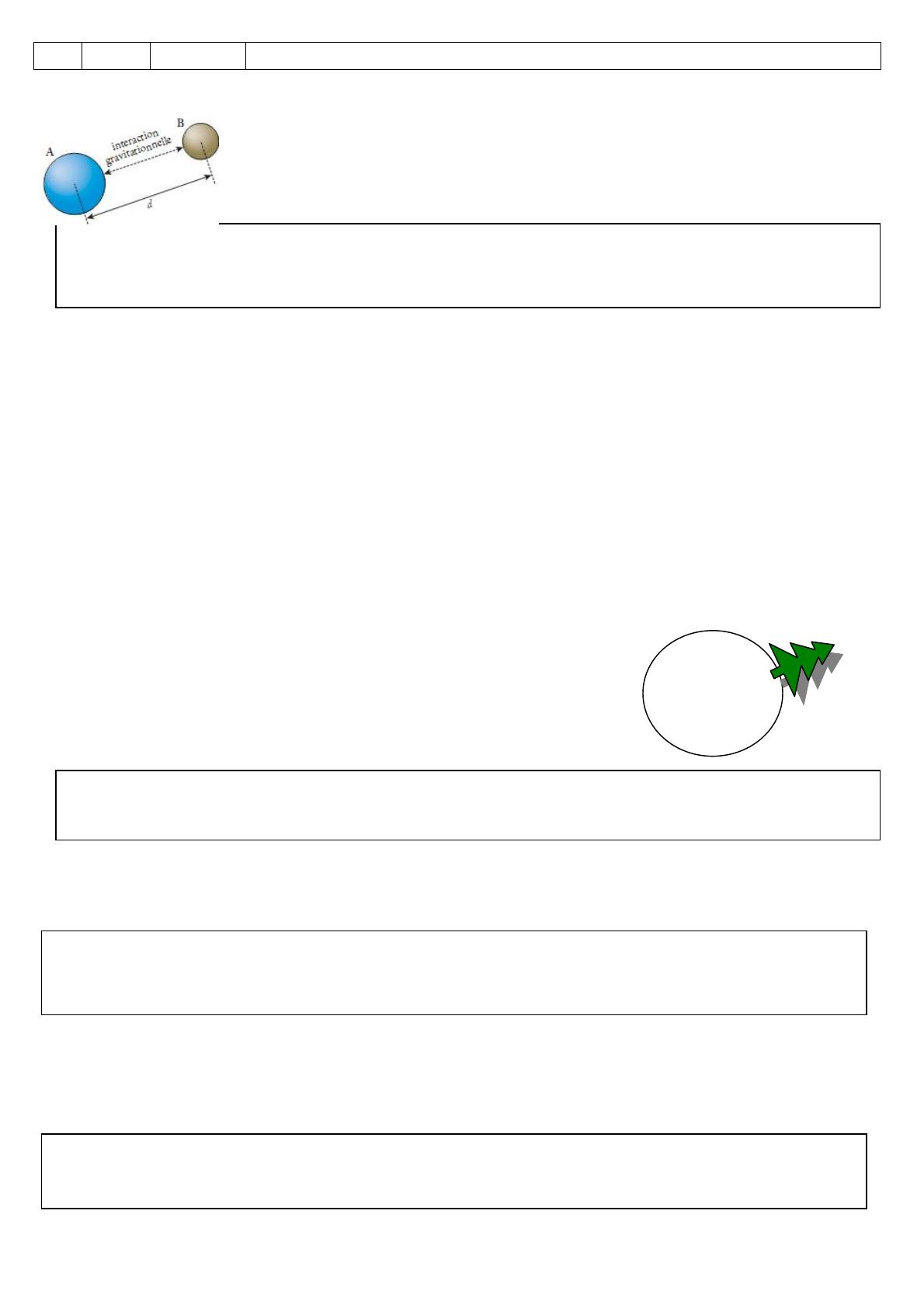
En 1687, Isaac Newton a énoncé la loi permettant de calculer la valeur de la
force de gravité exercée par un corps A sur un corps B, et également par le
corps B sur le corps A. Ces corps, séparés par la distance d, possèdent les
masses m
A
et m
B
. Cette loi se traduit par la relation :
Le poids d’un corps sur Terre résulte de l’action de l’attraction de
gravité exercée par la Terre sur ce corps.
Si m est la masse de ce corps, son poids P s’exprime par la
relation :

Henry Cavendich :Il isole l'hydrogène en 1766 et réalise en 1783 la
synthèse de l'eau par l'étincelle électrique. En 1798, il mesure, à l'aide
d'un appareil qu'il développe, la constante de gravitation et il en déduit la
masse de la terre. Sa balance de torsion est représentée sur l'image ci-
contre. En mesurant la très faible interaction entre 2 sphères de masse
différentes (une petite sphère de 729 grammes et une grosse sphère en
plomb de 158 kg) placées horizontalement, il en il en déduisit la première
mesure de la constante universelle de gravitation G, qu’il trouva égale à
6,75.10–11 N.m2 kg–2.
1
/
2
100%











