COSINUS d`un angle aigu dans un triangle rectangle

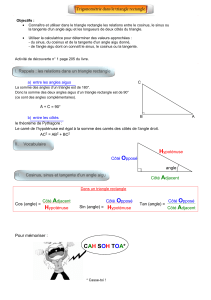
COSINUS d’un angle aigu
dans un triangle rectangle
Combien un triangle rectangle compte-t-il
 d’angle(s) droit(s) ? ……
 d’angle(s) aigu(s) ? ……
 d’angle(s) obtus ? ……
Existe-t-il une relation simple entre les longueurs et les angles ?
…………………………………………………………………………………………
…………………………………………………………………………………………
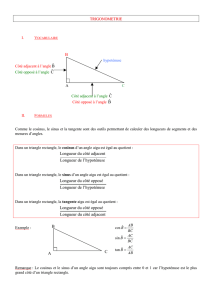
VOCABULAIRE
Dans un triangle rectangle, l’hypoténuse représente :
…………………………………………………………………………………………
…………………………………………………………………………………………
Dans un triangle rectangle, le côté adjacent à un angle aigu est :
………………………………………………………………………………………………………………………………
En ce sens, le côté « adjacent » c’est un peu le côté « voisin » !
hypoténuse
côté adjacent
à l’angle 
côté adjacent
à l’angle 

Construis, dans ce cadre, un triangle rectangle avec un angle de 30 ° .
Divise le côté adjacent à l’angle de 30° par l’hypoténuse de ton triangle .
Quel nombre trouves-tu ? ……

côté adjacent à un angle aigu
hypoténuse
Dans un triangle rectangle, le quotient du côté adjacent à un angle aigu
par l’hypoténuse est toujours constant . Cependant, ce nombre dépend
de l’angle aigu choisi !
Une explication ?
RETENIR
Si le triangle ABC est rectangle en A, on dispose de deux formules :
?= = ?
B
D
O
A
C

La touche COS de la calculatrice EN MODE DEGRES
La touche COS-1 de la calculatrice EN MODE DEGRES
BONUS
 en degrés
1 °
30 °
48 °
64 °
89,9 °
cos 
arrondi à 0,001
arrondi au degré
1 °
30 °
48 °
64 °
89,9 °
cos 
0,02
0,411
2/3
0,862
7/11
EXERCICE TYPE > TROUVER LA MESURE D’UN ANGLE AIGU
a) Exprimer le cosinus de l’angle 
 .
b) Déterminer la mesure arrondie au dixième, en degrés, de l’angle 
 .
EXERCICE TYPE > TROUVER LA LONGUEUR D’UN COTE
Calculer la longueur AC . On donnera l’arrondi au millimètre .

EXEMPLE DE SOLUTION
Jérémie et Mourad doivent déterminer les longueurs des côtés et tous
les angles du triangle rectangle représenté ci-dessous .
a) Jérémie a utilisé le théorème de Pythagore pour calculer AC, il a
ensuite construit la figure en vraie grandeur et mesuré les angles avec
son rapporteur . Rédige sa solution .
b) Hélas pour Mourad, la touche  de sa calculatrice ne marche plus !
Il a donc choisi une autre méthode : il a d’abord calculé 
 à 1° près,
puis en a déduit 
 et enfin AC . Rédige sa solution .
c) Compare les deux méthodes . Quelle est la meilleure solution ?