Symétrie et figures usuelles - Hachette

CHAPITRE
O
B
J
E
C
T
I
F
S
187
■ les axes de symétrie des figures usuelles.
■ les propriétés de la médiatrice d’un segment;
■ les propriétés des angles des figures usuelles;
■ les propriétés des diagonales des figures usuelles.
■ à la construction de la bissectrice d’un angle
au compas;
■ à la construction de figures usuelles.
Revoir :
Découvrir :
Symétrie
et figures usuelles
12
Appliquer :Appliquer :
Victor Vasarely est un peintre français d’origine hongroise (1908-1997).
Les œuvres de ce peintre sont géométriques et très colorées.
Vasarely s’amuse à déformer les perspectives, afin d’obtenir des effets optiques.
Combien d’axes de symétrie le tableau ci-dessus possède-t-il?
Combien d’axes de symétrie posséderait-il si l’on ne tenait pas compte de ses couleurs?
Victor Vasarely, Véga 200, 1968, coll. Michèle Vasarely
© E. Lessing/ AKG-images © ADAGP, Paris 2005.

JE DÉCOUVRE Trouver l’axe de symétrie d’un angle
3
JE DÉCOUVRE Énoncer les propriétés d’une médiatrice
2
J’AI DÉJÀ VU Trouver les axes de symétrie de quadrilatères
5
189
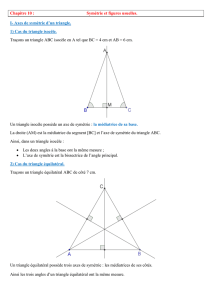
1) Tracer un triangle ABC isocèle en A. Construire la médiatrice (∆) de la base [BC].
a) Expliquer pourquoi le point A appartient à la droite (∆).
b) Quels sont les symétriques des points A, B et C par rapport à la droite (∆)?
c) Que représente la droite (∆) pour le triangle isocèle ABC ?
2) Nommer Ile milieu de la base [BC].
a) Quel est le symétrique de l’angle A
l
BI?
b) Que peut-on en déduire pour les angles A
l
BIet A
l
CI?
c) Recopier et compléter la phrase :
Dans un triangle isocèle, les ... à la base sont ... .
3) a) Quel est le symétrique de l’angle B
l
AI?
b) Que peut-on en déduire pour les angles B
l
AIet C
l
AI? Justifier la réponse.
c) Que représente la droite (∆) pour l’angle principal B
m
AC ?
4) Construire un triangle équilatéral. Tracer ses axes de symétrie.
12 Symétrie et figures usuelles
J’AI DÉJÀ VU Trouver les axes de symétrie d’un segment
1
188
Prendre une feuille de papier-calque et y tracer un segment [AB].
Déterminer, à l’aide de pliages, les axes de symétrie de ce segment.
Recopier et compléter la phrase :
Le segment [AB] admet ... axes de symétrie : l’un est la ... (AB), l’autre est la ... du segment [AB].
1) Tracer un segment [RS], ainsi que sa médiatrice (d).
Quel est le symétrique du point R par rapport à la droite (d)? Justifier la réponse.
2) Choisir un point T appartenant à la droite (d).
a) Quel est le symétrique du point T par rapport à la droite (d)?
b) Quel est le symétrique du segment [RT] par rapport à la droite (d)?
c) Que peut-on en déduire pour les longueurs RT et TS? Justifier la réponse.
d) Recopier et compléter la phrase :
Si un point appartient à la ... d’un segment, alors il est ... des extrémités du segment.
3) En utilisant un compas, construire sur cette figure un triangle RSU isocèle en U.
Faire une conjecture concernant le point U et la droite (d).
1) Décalquer la figure; [OA), [OB) et [OC) sont trois demi-droites.
2) Plier la feuille suivant la droite (OB).
a) Que peut-on constater concernant
les demi-droites [OA) et [OC) ?
b) Que représente la droite (OB) pour l’angle A
m
OC?
c) Que peut-on en déduire pour les angles A
m
OB et B
m
OC ? Justifier la réponse.
3) La droite (OB) partage l’angle A
m
OC en deux angles adjacents de même mesure.
Cette droite est appelée la bissectrice de l’angle A
m
OC.
La demi-droite [OB) est aussi la bissectrice de l’angle A
m
OC.
Siam affirme que la mesure de l’angle A
m
OC est la moitié de celle de l’angle A
m
OB.
Siam a-t-il raison?
ACTIVITÉS
➜
A
C
OB
Tu peux prolonger le tracé
des demi-droites [OA) et [OC).
J’ai recherché dans un dictionnaire le sens du mot « adjacent ».
JE DÉCOUVRE Énoncer des propriétés du triangle isocèle
4
J’ai utilisé une propriété de la médiatrice d’un segment.
■Partie 1.
1) Reproduire chaque quadrilatère sur une feuille de papier-calque.
2) Déterminer, à l’aide de pliages, ses axes de symétrie.
3) Tracer ses diagonales.
■Partie 2.
1) Citer les quadrilatères dont les diagonales semblent être portées par des droites perpendiculaires.
2) Citer ceux dont les diagonales semblent avoir la même longueur.
3) Citer ceux dont les diagonales semblent se couper en leur milieu.
Quadrilatère
Rectangle
Losange
Carré
Cerf-volant
Deltoïde
Une diagonale est un segment
qui relie deux sommets non consécutifs.
Les angles A
l
BIet A
l
CI
touchent la base [BC].

2
Bissectrice d’un angle
3
Axes de symétrie d’un triangle
190 191
aAxes de symétrie d’un segment
1
Médiatrice d’un segment aCas du triangle isocèle
Un triangle équilatéral possède trois axes de
symétrie : les médiatrices de ses côtés.
bCas du triangle équilatéral
Ainsi, les trois angles d’un triangle équilatéral
ont la même mesure.
COURS
➜
Un segment admet deux axes de symétrie :
➜la médiatrice de ce segment;
➜la droite qui porte ce segment.
La médiatrice du segment [AB] et la droite (AB)
sont les axes de symétrie du segment [AB].
■ Exemple :
A
B
(d)
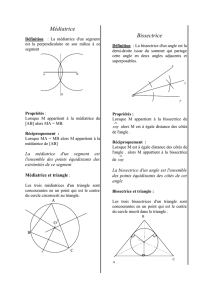
➜Si un point appartient à la médiatrice d’un
segment, alors il est à égale distance des extré-
mités de ce segment.
bPropriétés de la médiatrice d’un segment
■ Exemple :
➜Si un point est à égale distance des extré-
mités d’un segment, alors il appartient à la
médiatrice de ce segment.
La droite (d)
est la
médiatrice
du segment
[AB].
➜Si P (d), alors PA = PB.
➜Si PA = PB, alors P (d).
12 Symétrie et figures usuelles
Pour construire la médiatrice d’un segment [AB] :
➜on utilise un compas pour construire deux points C et D situés
à égale distance des points A et B ;
➜on trace la droite reliant ces deux points C et D.
La droite (CD) est la médiatrice du segment [AB].
cConstruction d’une médiatrice en utilisant un compas
Définition. La bissectrice d’un angle est la
droite, ou la demi-droite, qui partage cet angle
en deux angles adjacents de même mesure.
La demi-droite [OC) est la bissectrice de l’angle A
m
OB.
La droite (OC) est l’axe de symétrie de l’angle A
m
OB.
A
C
D
B
A
OB
C
Un triangle isocèle possède un axe de symé-
trie : la médiatrice de sa base.
4
Axes de symétrie d’un quadrilatère
aCas du cerf-volant
Définition. Un cerf-volant est un quadrilatère
ayant deux paires de côtés consécutifs de
même longueur et dont les diagonales se
coupent à l’intérieur.
Un cerf-volant possède un axe de symétrie : la
droite portant l’une de ses diagonales.
La droite (AI) est la médiatrice du segment [BC]
et l’axe de symétrie du triangle ABC.
■ Exemple :
A
I
(d)
C
B
Axe de symétrie
Angle principal
Angles à la base
Ainsi, dans un triangle isocèle :
➜les deux angles à la base ont la même mesure;
➜l’axe de symétrie est la bissectrice de l’angle principal.
■ Exemple :
■ Exemple :
I
J
L
K
IJKL est un cerf-volant.
La droite (IK) est son axe de symétrie.
Le quadrilatère EFGH est un cerf-volant.
Ainsi, comme la droite (FH) est son axe de symétrie :
•les droites (EG) et (FH) sont perpendiculaires;
•la droite (FH) est la bissectrice des angles E
m
HG et E
m
FG;
•les angles opposés F
m
EH et F
m
GH ont la même mesure.
E
G
H
F
Un angle possède un axe de symétrie : sa
bissectrice.
■ Exemple :
On a : A
m
OC = C
m
OB
(d)
A
B
P

JE RÉDIGE LA SOLUTION D’UN EXERCICE
Construire un rectangle FORT sachant que :
• ses diagonales se coupent en un point I.
•F
l
IO = 105° et IF = 2,5 cm.
Énoncé de l’exercice
Rédaction de la solution Mes conseils
PremIère éTape
DeUxième éTape
TroIsIème éTape
I
105°
FO
TR
2,5 cm
I
105°
FO
TR
2,5 cm
I
105°
J’utilise mon rapporteur
pour construire un angle de 105°.
193
Les diagonales d’un rectangle
se coupent en leur milieu
et ont la même longueur.
Donc : IO = IF = IR = IT = 2,5 cm.
Les points F, O, R et T sont donc
sur le cercle de centre I
et de rayon 2,5 cm.
Je commence par tracer
une figure à main levée
pour bien visualiser les données.
Je trace le rectangle demandé.
Et, surtout, je laisse
les traits de construction
et les codages qui m’ont permis
de le tracer.
12 Symétrie et figures usuelles
192
COURS
➜
Un losange a deux axes de symétrie : les droites
portant ses diagonales.
Ainsi, dans un losange :
➜les diagonales se coupent en leur milieu;
➜les droites portant les diagonales sont per-
pendiculaires;
➜les angles opposés ont la même mesure.
bCas du losange
Un rectangle a deux axes de symétrie :
les médiatrices de ses côtés.
Ainsi, dans un rectangle :
➜les côtés opposés ont la même longueur;
➜les diagonales se coupent en leur milieu;
➜les diagonales ont la même longueur.
Un carré a quatre axes de symétrie :
➜les droites portant ses diagonales ;
➜les médiatrices de ses côtés.
cCas du rectangle
dCas du carré
■Remarque : Les diagonales d’un carré ont la
même longueur, se coupent en leur milieu et
sont perpendiculaires.
■ Exemple :
■ Exemple :
■ Exemple :
A
DC
B
I
Centre du losange
O
A
A
B
B
D
D
C
C
Centre du
rectangle
On a déjà vu qu’un carré est à la fois un rectangle et un losange.
O
A
DC
B
Une figure peut avoir un ou plusieurs axe(s) de symétrie.
•Un axe de symétrie : le triangle isocèle et le cerf-volant.
•Deux axes de symétrie : le rectangle et le losange.
•Trois axes de symétrie : le triangle équilatéral.
•Quatre axes de symétrie : le carré.
F
I
O
TR
2,5 cm
105°
■Remarque : Les diagonales d’un rectangle ne
sont pas des axes de symétrie du rectangle.
■Remarque : Par abus de langage, on dit que les
diagonales d’un losange sont perpendiculaires.

Construire un losange ABCD tel que :
AC = 4 cm et BD = 7 cm.
Construire un losange EFGH tel que :
EG = 3,6 cm et FH = 4,8 cm.
Construire un rectangle EFGH de centre O
tel que : EG = 6 cm et E
m
OF = 70°.
Construire un rectangle MNOP de centre A
tel que : NP = 5,2 cm et N
m
AO = 97°.
Construire un carré MNOP tel que :
PN = 4,2 cm.
Construire un carré RSTU tel que : RT = 7,4 cm.
FACE est un cerf-volant dont les diagonales
se coupent en un point R.
Construire ce cerf-volant sachant que :
FC = 7 cm, FR = 2 cm et AE = 4 cm.
Construire un cerf-volant LKRS tel que :
LK = LS = KS = 5 cm et LR = 8 cm.
Reproduire en vraie grandeur les figures réali-
sées ci-dessous à main levée avec AC = 8 cm.
Tracer un triangle IJK rectangle en I tel que :
IJ = 2,1 cm et IK = 3,2 cm.
Construire les point L et M tels que le quadrilatère
JKLM soit un losange de centre I.
Tracer un triangle ABC isocèle en A tel que :
AB = 4,6 cm.
Construire les points D et E tels que le quadrilatère
BCDE soit un rectangle de centre A.
A
C
B
D
30°
D
EG
HF
3,2 cm
2,5 cm
195
Construire un losange LASO tel que : LS = 4 cm et AO = 2 cm.
Énoncé :
J’APPLIQUE
>
2
J’APPRENDS À...
Construire un quadrilatère
Solution :
12
12 Symétrie et figures usuelles
194
Construire la bissectrice de l’angle X
mm
OY sans utiliser
le rapporteur.
Énoncé :
Pour les exercices 1 à3, tracer l’angle donné, puis
construire sa bissectrice en utilisant le rapporteur.
aT
l
AV = 82° bB
m
OU = 104°
aG
m
HT = 116° bI
l
FR = 12°
aJ
l
FK = 135° bO
m
MH = 67°
Tracer un angle Z
l
LU mesurant 77°.
Construire, en utilisant le compas, la bissectrice de
cet angle.
Même consigne avec l’angle T
l
IC = 139°.
Construire en utilisant le compas la bissec-
trice d’un angle plat.
Comment vérifier le dessin obtenu?
1) Tracer un triangle ABC tel que :
AB = 6 cm, AC = 7 cm et BC = 8 cm.
2) Construire les bissectrices des angles de ce
triangle.
Reproduire, en utilisant le compas, les figures
ci-dessous et construire la bissectrice de l’angle M
m
PR.
1) Tracer un rectangle LONG tel que :
LO = 7 cm et ON = 5 cm.
2) Construire la bissectrice de l’angle L
m
ON.
3) Construire la bissectrice de l’angle N
m
LG.
Tracer un triangle BAF rectangle en A tel que :
BA = 7 cm et AF = 9 cm.
En utilisant le compas, partager l’angle A
m
BF en quatre
angles ayant la même mesure.
Construire un losange PILE tel que :
PI= 4,5 cm et P
k
IL = 120°.
Construire la bissectrice de chaque angle du losange.
PR
M
J’APPLIQUE
>
Solution :
1
J’APPRENDS À...
Construire la bissectrice d’un angle
1
5
6
2
3
4
SAVOIR-FAIRE
➜
X
Y
O
Je trace la droite (OC).
Cette droite
est la bissectrice
de l’angle X
l
OY.
Je trace un arc de cercle
de centre A et un arc de cercle
de centre B de même rayon.
Les deux arcs de cercle
se coupent en un point C.
Je trace un arc
de cercle de centre O :
il coupe les demi-droites
[OX) et [OY) aux points
A et B.
Je vais utiliser mon compas. J’obtiendrai une construction plus précise.
A
B
O
X
Y
A
B
OC
X
Y
A
B
OC
X
Y
P
M
R
7
8
9
10
Je fais un dessin à main levée.
Les données portent sur les diagonales [LS] et [OA].
Dans le cours, je trouve :
« les diagonales d’un losange sont perpendiculaires
et se coupent en leur milieu. »
A
O
LS
M
LS
M
LS
A
O
M
LS
Je trace un segment [LS]
de longueur 4 cm
et je nomme M son milieu.
Je trace la perpendiculaire
à la droite (LS) passant
par le point M.
Sur cette perpendiculaire,
je place les points A et O
à 1 cm du point M.
Je trace le losange LASO.
N’oublie pas de coder
ton dessin, pour expliquer
comment tu l’as construit.
13
14
15
16
17
18
19
20
21
22
11
Le centre d’un losange
ou d’un rectangle
est le point d’intersection
des diagonales.