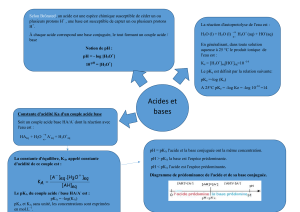
Chimie des solutions : cours sur les concentrations et dilutions

I. CHIMIE DES SOLUTIONS
1) SOLUTIONS
1.1) Définition : Une solution est un mélange homogène (constitué d’une seule phase)
de corps purs ne réagissant pas entre eux.
- Le corps qui est en plus grande proportion est appelé le solvant.
- Le ou les corps qu’on dissout dans le solvant constituent le ou les solutés.
Solution = Solvant + Soluté (s)
Exemple : NaCl dans l’eau ou le mélange NaCl + KCl dans l’eau.
Le soluté peut être un solide (exemple : NaCl) ou liquide (exemple : éthanol) ou un
gaz (exemple : CO2).
1.2) Solubilité et saturation.
La quantité de soluté que l’on peut dissoudre dans un solvant a une valeur maximale
limite pour une température et une pression données : C’et la solubilité du soluté dans ce
solvant, la solution est alors dite saturée et se présente en une seule phase (liquide). Si
l’on ajoute du soluté à une telle solution il apparaîtra deux phases (liquide +solide).
1.3) Nombre de moles d’un soluté
Le nombre de moles n d’un soluté ou d’une matière (en général) est défini comme étant le
rapport de la masse m du soluté ou de la matière à la masse molaire (M) de ce soluté ou
de cette matière M.
N = m/M
1.4) Expressions de la quantité de soluté dans une solution (concentration)
La quantité ou proportion d’un soluté dans une solution est appelée concentration. Il
existe différentes manières d’exprimer cette quantité de soluté dans une solution (ou
concentration).
1.4.1. Concentration massique ou titre pondéral ou teneur T
Elle correspond à la quantité de matière (quantité de soluté en grammes) dissoute dans 1
litre de solution. T (g/L)
T = m/V T en g/L
M= masse du soluté en g
V= Volume de la solution en L
1

1.4.2. Concentration molale ou molalité Cm
C’est la quantité de soluté (nombre de moles de soluté) dissoute dans 1 Kg de solvant.
Cm (mol/Kg).
Cm = n/ms Cm en mol/Kg
n= nombre de moles du soluté (en mol)
ms = masse du solvant en Kg
1.4.3. Concentration molaire ou molarité M
Elle correspond à la quantité de soluté (nombre de moles de soluté) dissoute dans 1 litre
de solution. M (mol/L).
M = n/V M= Molarité en mol/L
n= nombre de moles de soluté (en mol)
V = Volume de la solution en L.
Une solution molaire ou 1M = solution à 1 mol/L
Une solution 3M est équivalente à M = 3 mol/L ou molarité égale à 3 mol/L.
1.4.4 . Concentration équivalente ou normalité N
La normalité N ou concentration équivalente est le nombre d’équivalents grammes de
soluté dissout dans 1 litre de solution. N(eq.g/L).
N= n’/V N= normalité en eq.g/L
n’= nombre d’équivalents grammes de soluté.
V = Volume de la solution en L.
Notation : Solution normale = Solution de normalité égale à 1 eq.g/L
Solution 3N = solution de normalité égale à 3 eq.g/L
Nombre d’équivalents grammes d’un composé : C’est le rapport de la masse m de ce
composé (ou soluté) à la masse de l’équivalent gramme.
n’ = m/équivalent gramme
Equivalent gramme d’un composé : C’est la quantité en grammes de ce composé qui
met en jeu dans sa réaction ou sa dissolution 1 mole de protons H+ (acide) ou 1 mole d’
OH- (base) ou une mole d’électrons e-(oxydant ou réducteur).
2

Exemples de calcul de l’équivalent gramme
Acides : 1) HCl + KOH KCl + H2O
1 mole de HCl (36,5 g) correspond à la mise en jeu d’ 1 mole de H+ (qui réagit avec 1
mole de OH-) l’eq.g de HCl = la masse molaire de HCl = 36,5 g.
2) H2SO4 + 2 NaOH Na2SO4 + 2H2O
1 mole de H2SO4 (98 g) correspond à la mise en jeu de 2 moles de H+ (qui réagissent avec
2 moles de OH-) l’eq.g de H2SO4 = (la masse molaire de H2SO4)/2 = (98/2)g =
49 g.
Et de manière générale (pour un acide) :
Eq.g= masse molaire de l’acide / nombre de moles de H+ mis en jeu
Bases : 1) 3 Ba(OH)2 + 2 H3PO4 Ba(PO4) 2 + 6 H2O
3 moles de Ba(OH)2 (171 x 3 = 315 g) correspondent à la mise en jeu de 6 moles de OH-
L’eq. g de Ba(OH)2 = (3x masse molaire de Ba(OH)2)/ 6 = (masse molaire
de Ba(OH)2)/2
2) Ca(OH)2 + HCl Ca(OH)Cl + H2O
l’eq.g de Ca(OH)2 = masse molaire de Ca(OH)2
*Il faut remarquer dans ce dernier exemple qu’une mole de Ca(OH)2a mis en jeu 1 mole de
OH-. Si elle avait utilisé ses deux moles de OH- l’eq.g. aurait été égal à la masse molaire
divisée par 2.
Et de manière générale (pour une base) :
Eq.g = masse molaire de la base / nombre de moles de OH- mis en jeu
Oxydants et réducteurs :
10 FeSO4+ 2 KMnO4 + 8 H2SO4 5 Fe2(SO4)3 + 2 MnSO4 + K2SO4 + 8 H2O
FeSO4 est un réducteur (plus précisément Fe+2) qui en cédant un électron est oxydé en Fe+3
selon : Fe+2 Fe+3+ e-
Eq.g du réducteur FeSO4 = masse molaire de FeSO4
3

KMnO4 est un oxydant ou plutôt l’ion MnO4- qui est réduit en Mn+2 selon :
MnO4- + 8 H+ + 5 e- Mn+2 + 4 H2O
L’oxydant MnO4- (ou 1 mole de KMnO4) met en jeu 5 e- ou 5 moles d’électrons pour être
réduit en Mn+2 l’eq.g de KMnO4 = (masse molaire de KMnO4)/5
Et de manière générale, pour un oxydant ou réducteur :
Eq.g= masse molaire de l’oxydant ou réducteur /nombre d’électrons mis en jeu
Donc, dans tous les cas :
Eq.g. = masse molaire/i
Où i = nombre de moles de H+ ou de OH- ou d’électrons (e-) selon qu’il s’agit d’un acide,
d’une base, d’un oxydant ou d’un réducteur.
Remarque : Pour un monoacide (avec un seul H+ comme HCl) ou une monobase (avec un
seul OH- comme KOH) i=1 et dans ce cas eq.g = masse molaire.
1.4.5. Concentration exprimée en pourcentage poids (%).
C’est le nombre de parties (en poids) dans 100 parties (en poids) de la solution.
Exemple : Solution à 3% de NaCl signifie que 100 g de solution contiennent 3 g de NaCl et
97 g de solvant (eau).
Lors de la conversion de la concentration exprimée en % en concentration exprimée en
normalité ou en molarité il est indispensable de tenir compte de la densité relative (d) de la
solution :
d= m/V d= densité relative; m= masse de la solution et V= volume de la solution
d’où : m = dV
Exemple : Quelle est la molarité d’une solution de H2SO4 à 20% sachant que la densité
relative de cette solution est d=1,14.
1 litre de solution = 1000 mL a une masse m = dV = 1,14 x 1000 = 1140 g. Cette masse
contient une masse m1 d’acide égale à : m1= (mx20)/100= (1140 x 20)/100 = 228 g d’acide
(pur) H2SO4.
4

Molarité = n/V= m1/M V
Avec : M = 98 g. ; m1= 228g et V= 1L Molarité = M= 228/98x1 = 2,326 mol/L
1.4.6. Fraction molaire xi
Soit une solution ou mélange contenant n constituants (n composés) et soient ni = nombre de
moles du constituant i et xi sa fraction molaire dans le mélange (solution). Cette dernière est
définie comme suit :
xi= ni/Σni = ni/(n1+n2+….+ni+…nn)
ni= nombre de moles du constituant i
xi= fraction molaire du constituant i (sans dimension)
 Nous avons toujours Σ xi=1
1.4.7. Fraction massique wi
Soit une solution ou mélange contenant n constituants (n composés) et soient mi = masse du
constituant i et wi sa fraction massique dans le mélange (solution). Cette dernière est définie
comme suit :
wi= mi/Σmi = mi/(m1+m2+….+mi+…mn)
mi= masse du constituant i
xi= fraction massique du constituant i (sans dimension)
 Nous avons toujours Σ wi=1
1.4.8. Relations entre les concentrations
a) Relation entre molarité (M) et normalité (N).
N= (nombre d’équivalents grammes)/Volume (Litre) ……..(1)
Nombre d’équivalents grammes = masse / Eq. g = masse / (masse molaire /i) = i x
(masse/masse molaire) = i x nombre de moles = i x n
On remplace dans (1) le nombre d’équivalents grammes par i x n et on obtiendra :
5