Mécanique Générale: Exercice Disque dans un Cerceau - IMT Mines Alès

IMT Mines Alès – Formation d’Ingénieurs généralistes - 2ème Année 2024-2025
Mécanique Générale
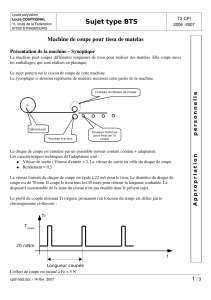
Exercice: Disque dans un cerceau
Un disque (D) de centre G et de rayon R et de masse m, roule à l'intérieur d'un cerceau (C) de centre
O et de rayon 3R.
R0(O,x0,y0,z0) un repère lié à (C) est fixe
R(G,x,y,z)est un repère lié à (D) mobile/à R0
R1(O,u,v,z0) un repère intermédiaire.
I un point de contact entre (D) et (C)
OO
Le moment d'inertie /ox: IGx = A I
Le moment d'inertie /oy: IGy = B
Le moment d'inertie /oz: IGz = C
Partie A-Etude cinématique
1- Donner le vecteur taux de rotation de R1/R0, le vecteur taux de
rotation de R/R1, et le vecteur taux de rotation de D/R0,
2-Donner les éléments de réduction du torseur cinématique du disque /R0
au point G
3- Quel est le plan tangent au disque et au cerceau au point I
4- Calculer la vitesse de glissement de (D)/(C) au point de contact I
5- Quelle est la condition de roulement sans glissement
Partie B- Géométrie des masse-Cinétique:
Dans les conditions du roulement sans glissement:
6- Expliquer pourquoi la matrice d'inertie du disque au point G dans R(x,y,z) est symétrique, donner
cette matrice en fonction de A, et C.
7- Comment en appel cette matrice, R(G,x,y,z), A et C
8- Calculer A en fonction de C
9-Calculer C en fonction m et R et donner la matrice d'inertie du disque au point G
10 -Donner les éléments de réduction du torseur cinétique du disque (D) au point G /R0
Partie C- Dynamique et énergie:
Dans les conditions du roulement sans glissement (liaison parfaite)
11- Donner les éléments de réduction torseur dynamique du disque (D) au point G/R0
12- Calculer l'énergie cinétique du disque (D).
13-Montrer qu'il y a conservation de l'énergie mécanique et écrire la relation correspondante
"intégrale première", on désignera par m l'amplitude maximale des oscillation (m </2). Exprimer
cette relation on fonction de m, R, etm.
O
O
G

14- Dans le cas particulier où  reste petit. Etablir une équation différentielle du second dont  est
solution . Déterminer la période des petites oscillations.
15- Donner les éléments de réduction torseur des efforts extérieurs du disque (D) au point G/R0, et
calculer la puissance de ces efforts.
16-Par application du théorème de l'énergie cinétique trouver les équations différentielles du
mouvement que remarquez vous?.
Partie D: mouvement avec frottement
17- Dans le cas générale, par application du théorème de la résultante dynamique, Déterminer les
expressions des composantes normales N et tangentielle T de la réaction du disque (D).
On tenant compte du résultat obtenue à la question 13-, indiquer comment les composantes varient
avec  et montrer pour qu'il y ait toujours roulement sans glissement, le coefficient de frottement de
glissement f doit être supérieur à une valeur fonction de m que l'on précisera.