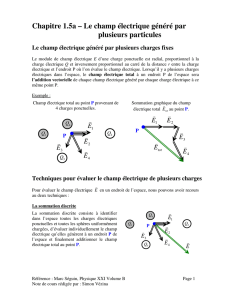
Mouvement d'une particule dans un champ électrique uniforme

Référence : Marc Séguin, Physique XXI Tome B Page 1
Note de cours rédigée par Simon Vézina
Chapitre 1.14 – Le mouvement d’une particule dans
un champ électrique uniforme
L’accélération d’une particule chargée dans un champ électrique
Une particule chargée plongée dans un champ électrique subit une accélération
a
v
dont le module est
égal au produit de la charge q de la particule avec le module du champ électrique
E
v
le tout divisé par
la masse m de la particule. L’orientation de l’accélération dépend de l’orientation du champ électrique
E
v
et du signe de la charge q :
m
Eq
a
v
v=
où
a
v
: Accélération de la particule chargée (m/s
2
)
q : Charge électrique de la particule (C)
E
v
: Champ électrique constant (N/C)
m : Masse de la particule (kg)
Preuve :
Évaluons l’accélération d’une particule de masse m et de charge q plongé dans un champ électrique
arbitraire
E
v
à partir de la 2
e
loi de Newton :
amF
v
v
=
∑
⇒
amF
v
v
=
e
(Seulement la force électrique
e
F
v
)
⇒
amEq
v
v
= (Remplacer EqF
v
v
=
e
)
⇒
m
Eq
a
v
v
= ■ (Isoler
a
v
)
Accélération dans un champ électrique uniforme
Lorsqu’une particule chargée est plongée dans un champ électrique uniforme
y
E , elle subit alors une
accélération constante
y
a . Ainsi, les équations du mouvement de la particule se résument aux
équations du MUA (mouvement uniformément accéléré).
Si la particule se déplace en deux dimensions, la forme de la trajectoire sera alors une parabole
1
:
• 0=
x
E
• constant =
y
E
⇒
0 =
x
a,
m
qE
a
y
y
=
• tvxx x00 +=
• tavv
yyy
+=
0
•
2
00
2
1tatvyy yy ++=
•
)(2
0
2
0
2
yyavv
yyy
−+=
1
Cette situation est comparable au mouvement d’un projectile sous l’effet d’une gravité constante.
0
1
>q
0
2
<q
E
v
2
a
v
1
a
v

Référence : Marc Séguin, Physique XXI Tome B Page 2
Note de cours rédigée par Simon Vézina
Situation A
:
Un électron dans un accélérateur
.
Un électron, initialement au repos, est accéléré entre
deux plaques, dans un champ électrique d’intensité 10
5
N/C. On désire (a) évaluer le temps qu’il faudra
pour atteindre la vitesse de 0,2c (c’est la vitesse de la lumière et elle vaut 3x10
8
m/s) et (b) la distance
qu’il aura alors parcourue ?
Supposons la situation suivante où le champ électrique est orienté selon l’axe x négatif :
N/C101
5
iiEE
v
v
v
×−=−=
Appliquons la 2
ième
loi de Newton à l’électron afin d’évaluer l’accélération :
amF
v
v
=
∑
⇒
amF
v
v
=
e
(Force électrique seulement)
⇒
m
Eq
a
v
v= ( EqF
v
v
=
e
et isoler
a
v
)
⇒
(
)
(
)
( )
31
519
1011,9
101106,1
−
−
×
×−×−
=i a
v
v (Remplacer valeurs num.)
⇒
216
m/s10756,1 ia
v
v
×= (Évaluer
a
v
)
Évaluons le temps requis pour atteindre la vitesse de 0,2 c à l’aide des équations du MUA selon l’axe x :
tavv
xxx
+=
0
⇒
(
)
(
)
(
)
t
168
10756,101032,0 ×+=×∗ (Remplacer valeur num.)
⇒
s10417,3
9−
×=t
(a) (Calcul)
Évaluons la distance parcourue par l’électron : ( xx
=
∆
car 0
0
=x )
2
00
2
1tatvxx
xx
++=
⇒
( ) ( )
(
)
(
)
(
)
2
9169
10417,310756,1
2
1
10417,300
−−
××+×+=x
⇒
m10,0=x (b)

Référence : Marc Séguin, Physique XXI Tome B Page 3
Note de cours rédigée par Simon Vézina
Situation B
:
Un électron entre deux PPIUC
.
Un électron
pénètre horizontalement entre deux PPIUC de longueur L
séparée par une distance h, avec une vitesse initiale v
0
tel
que montré ci-contre. On désire évaluer l’expression du
module du champ électrique E permettant à l’électron de
sortir du système de plaques en frôlant la plaque supérieure.
(Négliger la force gravitationnelle, car la masse de l’électron
est trop faible.)
Voici l’expression du champ électrique selon notre système d’axe :
jEE
v
v
−=
Appliquons la 2
e
loi de Newton à l’électron :
amF
v
v
=
∑
⇒
amF
v
v
=
e
(Force électrique seulement)
⇒
m
Eq
a
v
v
= ( EqF
v
v
=
e
et isoler
a
v
)
⇒
(
)
(
)
( )
e
m
jEe
a
v
v−−
= (Remplacer valeurs)
⇒
j
m
Ee
a
v
v
e
=
(Évaluer
a
v
)
Appliquons l’équation du MUA au mouvement selon l’axe x et évaluons le temps pour traverser les
deux plaques : ( 0 =
x
a )
2
00
2
1
tatvxx
xx
++=
⇒
( ) ( ) ( ) ( )
2
0
0
2
1
0 ttvL ++= (Remplacer paramètres)
⇒
0
v
L
t=
(Isoler t )
Appliquons l’équation du MUA au mouvement selon l’axe y :
2
00
2
1
tatvyy
yy
++=
⇒
( ) ( ) ( )
2
e
2
1
00 t
m
Ee
th  ++= (Remplacer tout sauf t )
⇒
2
0e
2
1
=v
L
m
Ee
h (Remplacer t)
⇒
2
2
0e
2
eL
vhm
E=
(Isoler E )

Référence : Marc Séguin, Physique XXI Tome B Page 4
Note de cours rédigée par Simon Vézina
Tube cathodique
CRT monitor
Déflexion par plaque chargée
(champ électrique)
Déflexion par courant électrique circulant
dans des bobines de fil conducteur
(champ magnétique)
(tube dans un oscilloscope)
(tube dans une télévision)
Exercices
1.14.11 Une incursion dans un champ électrique
uniforme. Sur le schéma ci-contre, chaque carreau mesure
10 cm de côté. Dans la moitié de gauche, le champ
électrique est nul ; dans la moitié de droite règne un champ
électrique uniforme orienté vers la droite. Un électron est
lancé à partir du point A : 0,2 µ s plus tard, il pénètre dans
le champ électrique au point B . (a) Sachant que l’électron
ressort du champ électrique au point C , déterminez le
module du champ. (b) Décrivez un montage réel qui
pourrait créer le champ électrique représenté.

Référence : Marc Séguin, Physique XXI Tome B Page 5
Note de cours rédigée par Simon Vézina