TP : Mesures et calculs d'incertitudes en physique

TP6 ⋆Mesures et calculs d’incertitudes
Objectifs du TP
⋆Acquérir la méthode de calculs d’incertitudes et la rédaction associée
⋆Simuler un processus aléatoire permettant de caractériser la variabilité de la
valeur d’une grandeur composée (méthode de Monte-Carlo)
⋆Comparer deux mesures à l’aide de leur écart-type normalisé (z-score)
⋆Présenter le résultat d’une mesure
I Position du problème
Le résultat d’une mesure est un ensemble de valeurs numériques accompagné d’une unité appro-
priée, raisonnablement attribuables à la grandeur d’intérêt (appelé mesurande). Le résultat d’une
mesure n’est donc pas une valeur unique !
Mesure
La valeur mesurée est une valeur particulière de cet ensemble, c’est la meilleure estimation possible du
mesurande.
La notion de « mesure » a plusieurs significations dans la langue française. C’est donc délicat de l’utiliser de
façon univoque. En physique-chimie, une mesure est la procédure expérimentale qui conduit à attribuer un
ensemble de valeurs numériques à une grandeur d’intérêt. La valeur lue sur un appareil de mesure n’est donc
pas directement une mesure. . . Nous parlerons d’observation ou d’indication pour éviter toute confusion.
Par exemple, la valeur lue sur l’écran d’un voltmètre est une observation (et non pas une mesure). La
question au groupe de TP voisin « T’as mesuré combien pour la tension ? » nécessite donc répondre par un
ensemble de valeurs (cf. définition d’une mesure ci-dessus) alors que la réponse à « T’as observé combien
pour la tension ? » peut entrainer une réponse unique.
Nous utiliserons la notion de variabilité pour décrire le fait qu’un résultat de mesure ne peut être
unique.
Variabilité
Cette variabilité peut provenir de nombreux aspects, dont les principaux sont les suivants :
— le choix de la méthode de mesure ;
— aux variations de l’environnement ;
— aux instruments de mesure ;
— au processus physique lui-même ;
— et surtout, à la personne réalisant l’expérience.
Généralement au niveau scolaire, la personne réalisant l’expérience est la principale cause de variabilité de
la mesure. Par ses gestes, ses choix et sa technique, cette personne introduit une variabilité importante. Il
est donc totalement naturel que deux personnes réalisant la même expérience, dans les mêmes conditions,
avec le même matériel, trouvent des valeurs différentes.
Il est à noter que le but de toute formation expérimentale, de la maternelle jusqu’au plus haut niveau
universitaire et professionnel, permet patiemment de faire diminuer cette variabilité.
L’incertitude est une indication de la dispersion de l’ensemble des valeurs raisonnablement attribuables à
la grandeur d’intérêt.
L’incertitude-type est une incertitude évaluée à l’aide d’un écart-type.
MP 2024|25 Lycée H. Poincaré 1/7
TP6

L’incertitude-type est une évaluation de l’écart-type de l’ensemble des grandeurs raisonnablement
attribuables à la grandeur d’intérêt. L’incertitude-type quantifie la variabilité d’une mesure. Nous
noterons l’incertitude-type u(uncertainty en anglais).
Incertitude-type
II Approche statistique : évaluation de type A de l’incertitude
L’évaluation de type A de l’incertitude correspond au cas où l’on dispose de nobservations supposées
indépendantes d’une même grandeur d’intérêt. Nous nous placerons dans le cas où n⩾10 pour
assurer la validité de l’approche statistique de cette méthode.
La valeur mesurée correspond alors à la valeur moyenne des observations et l’incertitude-type associée
à cette moyenne correspond à l’écart-type sde la distribution divisé par la racine carrée du nombre
d’observation.
u=s
√n
Type A
Statistique sur un résistor
On réalise n= 30 mesures (supposées indépendantes) de la résistance d’un même résistor. On obtient le
tableau de mesures suivant (en Ω) :
101,8 99,6 100,1 99,4 100,4 99,2 100,3 98,7 100,5 100,7
99,7 100,5 99,7 99,3 99,8 100,0 100,9 99,8 100,0 100,0
100,9 100,0 100,5 99,2 99,6 99,9 100,4 100,5 100,2 100,4
II.1 Utilisation d’un tableur
Rentrer ces valeurs dans un tableur Excel ou LibreOffice. Nous utiliserons les fonctions MOYENNE() et
ECARTYPE().
Manip.
II.1.a Estimation de l’espérance mathématique de la population
La valeur moyenne de l’échantillon, définie pour un ensemble de nmesures {X1,X2,...,Xn}, est donné par
X = 1
n
n
P
i=1
Xi
Calculer la résistance moyenne Rm.
Manip.
Faute d’informations supplémentaires, nous choisirons comme estimateur de la résistance la moyenne 1de
l’échantillon, soit Rm= R .
II.1.b Distribution des mesures
Il convient maintenant d’évaluer la distribution des valeurs des résistances autour de la valeur moyenne.
Pour cela on introduit une nouvelle grandeur : l’écart-type de la population, qui pour être calculée nécessite
la connaissance de toutes les résistances. On peut néanmoins l’estimer à l’aide d’une grandeur nommée
« l’estimateur de l’écart-type de la population » que l’on évalue à partir des mesures effectuées et défini
par
s=s1
n−1
n
P
i=1
(Xi−X)2=v
u
u
t1
n−1"n
P
i=1
Xi2−1
nn
P
i=1
Xi2#
L’écart-type est une mesure de la dispersion des valeurs mesurées par rapport à la valeur moyenne. Plus
l’écart-type est petit, plus les mesures sont resserrées autour de la valeur moyenne et inversement (voir un
exemple sur la figure 1).
1. Rmconstitue une estimation de l’espérance mathématique de la variable aléatoire R.
MP 2024|25 Lycée H. Poincaré 2/7

X X
2s2s2s2s
0
20
40
60
80
100
120
140
160
180
200
880 920 960 1000 1040 1080 1120
0
20
40
60
80
100
120
140
160
180
200
880 920 960 1000 1040 1080 1120
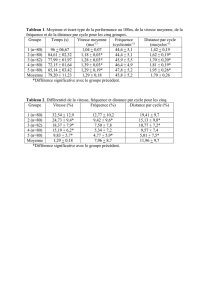
Figure 1 – Sur les deux figures ci-dessus est représentée la distribution sous la forme d’un histogramme
de deux échantillons de 1000 résistances prélevées dans deux populations différentes. En abscisses est
représentée la valeur de la résistance (en Ω), en ordonnées le nombre de résistances possédant cette valeur.
Les deux échantillons ont une valeur moyenne de 1000 Ω. En revanche, l’échantillon de gauche possède un
écart-type de 10 Ω et celui de droite de 30 Ω. On voit bien que les valeurs des résistances de l’échantillon
de gauche sont plus « resserrés » autour de la valeur moyenne que pour l’échantillon de droite
Calculer un estimateur de l’écart-type, sR, associé à votre échantillon de valeurs de résistances.
Manip.
II.1.c Incertitude sur l’espérance mathématique
Nous avons estimé l’espérance mathématique de la population des résistances à l’aide de la valeur moyenne
des nmesures effectuées. Mais avec quel degré de confiance cette estimateur approche-t-il l’espérance de
la population ? Si l’on fait l’hypothèse que les nmesures sont indépendantes et suivent la même loi, alors
nous pouvons montrer que l’écart-type sur la valeur moyenne est égal à l’écart-type sur la variable aléatoire
divisé par √n. On définit donc l’incertitude-type sur Rpar uR=sR
√n.
Calculer numériquement l’incertitude-type associée à R,uR.
Manip.
II.1.d Présentation du résultat
Xm=. . . unités ; uX=. . . unités
Il est recommandé dans le domaine de la métrologie de ne conserver que les deux premiers chiffres signifi-
catifs (CS) pour l’incertitude-type. De plus, le dernier chiffre significatif de la valeur mesurée Xmdoit être
à la même position décimale que pour l’expression de l’incertitude.
Par exemple, R = 40,12 Ω
| {z }
précision au 1/100 d’ohm cf. CS
;uR= 0,88
|{z}
2 CS
Ω.
Présenter votre résultat sous la forme indiquée ci-dessus.
Manip.
MP 2024|25 Lycée H. Poincaré 3/7
TP6

II.2 Utilisation de Python
Reprendre l’ensemble de la démarche précédente créant un script sous Python. Nous utiliserons
Pyzo comme environnement et nous aurons besoin du module numpy (import numpy as np). Nous
utiliserons les fonctions np.mean() et np.std(, ddof = 1) a. Nous utiliserons un numpy array
np.array([101.8,99.6,... ] pour la liste des valeurs de la résistance.
a.std pour standard deviation qui est l’écart-type en anglais et ddof = 1 pour calculer l’écart-type « n−1»
Manip.
III Cas de la mesure sans variabilité observée, évaluation de type B de l’in-
certitude
Nous nous plaçons ici dans le cas d’une observation unique, ou bien dans le cas où la répétition des
observations conduit exactement à la même valeur (pas de variabilité observée).
L’incertitude-type associée à une observation unique exprime la variabilité potentielle d’une observa-
tion. Elle quantifie les fluctuations typiques d’une observation à l’autre.
Type B
Au niveau CPGE, il parait souhaitable de se restreindre à deux situations simples :
— Si on n’a aucune autre information qu’une limite basse et une limite haute pour la grandeur d’intérêt,
alors on suppose que la répartition est uniforme entre ces deux bornes (loi de probabilité uniforme
ou rectangulaire).
— Si on connait la valeur mesurée et l’incertitude-type associée, mais qu’on ne connait pas la distribution
sous-jacente, alors on suppose que la distribution est gaussienne (loi normale).
Lorsqu’on utilise un appareil de mesure, différents cas peuvent apparaitre :
— le constructeur de l’appareil de mesure fournit directement l’incertitude-type ou l’étendue d’un in-
tervalle de confiance dans la notice (cas rare) →on fera l’hypothèse gaussienne ;
— le constructeur fournit une « incertitude constructeur », ou « précision », sans explicitation ; on décide
par convention qu’il s’agit de la demi-étendue d’un intervalle de valeurs possibles →on fera l’hypothèse
d’une loi rectangulaire et l’incertitude-type est donnée par la demie-étendue divisée par racine de 3 ;
si nous notons ala demi-étendue, nous aurons
u=a
√3ou bien u=2a
2√3=2a
√12 =max −min √12 avec 2al’étendue
— le constructeur ne fournit rien, il faut évaluer cet appareil à l’aide d’autres instruments de mesure.
⋆Avec une règle ou une burette : dans de bonnes conditions, nous pouvons nous limiter à une
étendue qui correspond à une graduation. Ainsi, pour une règle graduée en mm, nous avons
u=1
√12 = 0,29 mm.
⋆Pour un appareil numérique (voltmètre ou balance par exemple), nous trouvons souvent une précision
qui est la valeur de la demi-étendue. Par exemple, une tension U=2,1273 V est donnée avec une pré-
cision de 0,5%. Ainsi, u= 2,127×0,5
100 ×1
√3= 6,1 mV. Parfois, il est donné une précision sous la forme
p% lecture + nUL. UL signifie Unité de Lecture, nous trouvons aussi UR Unité Représentative ou
encore D pour Digits. Cette grandeur correspond à la plus petite valeur affichable sur l’appareil dans le
calibre donné, c’est la résolution de l’appareil qui dépend du calibre. Par exemple, 0,5 % lecture+8 UL
avec une résolution de 0,1 mV conduit à u=2,127 ×0,5
100 + 8 ×0,1.10−3×1
√3= 6,6 mV.
⋆Sur une pipette jaugée, il est indiqué la demie-étendue de l’intervalle. Par exemple, nous avons des
Quelques exemples
MP 2024|25 Lycée H. Poincaré 4/7

pipettes de 25 mL avec +
−0,030 mL. Ainsi, u=0,03
√3= 0,017 mL. Pour rappel, le volume d’une goutte
est d’environ 0,05 mL.
III.1 Mesure directe
Mesurer une résistance de 1 kΩ au multimètre. Indiquer la gamme du multimètre. Indiquer
l’incertitude-type sur cette mesure à l’aide de la documentation du multimètre.
Régler l’alimentation stabilisée sur 0,3 V. Mesurer cette tension au multimètre sur la gamme mV puis
sur la gamme V. Indiquer l’incertitude-type pour ces deux mesures.
Conclure quant au choix du calibre.
Manip.
III.2 Incertitude-type composée
Il existe, cependant, un grand nombre de cas où la grandeur à évaluer résulte d’un combinaison de plusieurs
mesures faites avec différents appareils.
Cas particuliers à retenir :
— si, et seulement si,fest de la forme
f(Y1,...,Yn) = kY1α1Y2α2...Yn
αn
où ket les αisont des constantes réelles, alors
u(X)
|X|=sn
P
i=1 αi
u(Yi)
Yi2
— dans le cas d’une somme x=a+bou d’une différence x=a−b, on a
u(x) = qu(a)2+u(b)2
— dans le cas d’un produit x=ab ou d’un quotient x=a/b, on a
u(x)
|x|=su(a) a2
+u(b)
b2
III.2.a Exemple : mesure d’une résistance par la loi d’Ohm
1. Choisir une résistance de valeur constructeur 1 kΩ.
2. L’alimenter en courant continu sous une tension de l’ordre de 1 V.
3. À l’aide d’un ampéremètre et d’un voltmètre, mesurer précisément, courant I et tension U aux
bornes de la résistance ainsi que les incertitudes-type sur ces valeurs (en se référant à la notice).
4. En déduire l’incertitude-type sur la mesure de la résistance.
Manip.
III.2.b Simulation de Monte-Carlo
Dans les cas plus complexes qu’un simple produit, il est très utile de recourir à une simulation de Monte-
Carlo pour estimer l’incertitude-type u. La méthode est la suivante : nous allons réaliser un « grand
nombre » de tirages au sort numériques en respectant les lois de probabilité pour les différentes grandeurs
qui interviennent dans notre problème puis mener une étude statistique (calcul de moyenne et d’écart-type).
Nous allons nous entrainer à cette méthode en reprenant le cas précédent où U et I suivent des lois
rectangulaires. Pour chaque tirage au sort, nous calculerons la résistance associée R = U/I. La valeur de
R mesurée sera la valeur moyenne des résistances obtenues après un grand nombre de tirage au sort et
l’incertitude-type sera l’écart-type de la distribution obtenue.
MP 2024|25 Lycée H. Poincaré 5/7
TP6