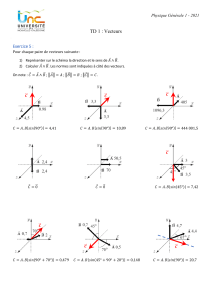
Calculs vectoriels et différentiels : Cours de mécanique

Cours de Mécanique, Pr M. ZOUNGRANA , UFR-SEA/U.O (first draft) Page 1
Chapitre 1: Calculs vectoriels et différentiels
I. Vecteurs, base et repère
1. Les vecteurs
a. Norme d’un vecteur
L’espace de la mécanique est l’espace E3, espace affine associé à R3. L’espace des vecteurs utilisé
est l’espace vectoriel réel euclidien de dimension 3 noté E3. Un vecteur sera noté
u
et sa longueur
u
norme de
u
.
Soit vecteur
abu
constitué par le coulpe de points (a,b). La norme du vecteur
abu
est donc la
distance d(a,b) des 2 points du couple représentant le vecteur libre. La norme d’un veteur est une
application qui vérifie les propriétés suivantes :
- P1 :
0u 
0u 
- P2:
ukuk ,E u IR, k 3
- P3 :
v uv u ,E v et u 3
- Si
kujuiuu 321 
,
2
3
2
2
2
1uuuu 
D. Un vecteur
v
dit normé ou unitaire si norme égale à l’unité :
1v 
.
Remarque : Un vecteur libre est normé en divisant ses composantes par la norme. On peut donc écrire
un vecteur normé sous la forme :
v
v
i ,E v v
3
v
i vv 
.
b. Angle de deux vecteurs
Soit deux vecteurs libres
u
et
v
(
abu
et
'abv
). L’angle non orienté des deux vecteurs
u
et
v
est
l’angle des demi-supports de leurs représentants (a, b) et (a, b’). Il est noté
v,u
.
est un angle non orienté.
Cet angle est mesuré habituellement en radians et tel que
0
c. Cosinus directeurs
Soit
,, kji
une base orthonormée de l’espace vectoriel V. Un vecteur libre
v
de V est repéré par
rapport aux vecteurs de la base par 3 angles :
i,v
,
j,v
,
k,v
.

Cours de Mécanique, Pr M. ZOUNGRANA , UFR-SEA/U.O (first draft) Page 2
Dans une base orthonormée les composantes de
v
sont :
cos vv1
;
cos vv2
;
cos vv3
.
Les cosinus directeurs de
v
sont:
v
v
cos 1
;
v
v
cos 2
;
v
v
cos 3
En écrivant que
2
3
2
2
2
1
2vvvv 
, on obtient la relation fondamentale entre les cosinus
directeurs dans un repère orthonormé :
1coscoscos 222 
.
2. Base
Une base de E3 est un ensemble de trois vecteurs non coplanaires; nous la noterons
,, kjiB
ou B
tout simplement.
Remarque : Dans le cas d’une base orthonormée directe de vecteurs de base
,, kji
on a :
1 kji
0 ikkjji
1 kkjjii
 Les vecteurs
kji et ,
forment un
trièdre direct.
3. Repère
 Un repère de E3est l’ensemble d’un point de E et d’une base de E3. Nous noterons un tel repère
,,, kjiO
ou
,,, kjiOR
ou
R
. Les composantes dans le repère
,,, kjiOR
d’un vecteur
u
sont les composantes
321 ,, uuu
de
u
dans la base
,, kjiB
.
kujuiu 321 u 
II. Produit scalaire
Le produit scalaire de deux vecteurs
u
et
v
de composantes respectives
321321 v,v,v et u,u,u
dans le repère orthonormé direct R est égal à :
vu 
.
- Expression à partir des composantes des vecteurs :
332211
332211
321321
vuvuvu
kkvujjvuiivu
kvjvivkujuiuvu

Cours de Mécanique, Pr M. ZOUNGRANA , UFR-SEA/U.O (first draft) Page 3
- Expression à partir des normes et l’angle formé par les deux vecteurs
On a :
vuvuvu  cos
NB : Le vecteur unitaire
v
e
d’un vecteur
v
est :
III. Le produit vectoriel
1. Définition
Soient deux vecteurs
u
et
v
, et soit α l’angle formé par ces deux
vecteurs : .
Le produit vectoriel des deux vecteurs
u
et
v
de composantes
respectives dans le repère orthonormé
direct R est noté
vu 
. Il est égal :
- au vecteur
0
si
u
et
v
sont colinéaires, ou si
vu 
(
0 uu
)
- au vecteur de longueur
v,usinvu 
, perpendiculaire au plan
vu,
et orienté de tel sorte
que la base
vuvu ,,
soit direct si
u
et
v
ne sont pas colinéaires.
Dans une base orthonormée direct
,, kjiB
la définition du produit vectoriel entraine :
0 0 0 kkjjii
jikikjkji
NB :
vu 
=
uv 
 Expression à partir des composantes des vecteurs :
kvuvujvuvuivuvu
kkvujkvuikvu
kjvujjvuijvukivujivuiivu
kvjvivkujuiuvu
122131132332
332313
322212312111
321321
Autre façon de l’exprimer :
1221
3113
2332
3
2
1
3
2
1
vuvu
vuvu
vuvu
v
v
v
u
u
u
vu
- Expression à partir des normes et l’angle formé par les deux vecteurs
sin , uv u v u v u v i 
Remarque : Si
0 vu
, l’une au moins des trois propriétés suivantes est vérifiée :
v
v
ev
v,u
321321 v,v,v et u,u,u

Cours de Mécanique, Pr M. ZOUNGRANA , UFR-SEA/U.O (first draft) Page 4
vuvu et ; 0 , 0 
sont colinéaires.
Application: Le moment d’une force
Le moment d’une force 
par rapport à un point O est un produit vectoriel. Si A est le point
d’application de la force, son moment est : 
.
Le moment mesure la capacité d’une force à faire tourner un solide
comme l’illustre la figure ci-contre :
- la force 
, dont le moment par rapport à O est nul, ne peut
faire tourner le boulon ;
- la force 
exercera un moment plus important que la force 
.
2. Double produit vectoriel
Quels soient les vecteurs
wet , vu
, les deux propriétés suivantes vérifiées :
wvuwuvwvu
vuwwuvwvu
..
..
Application: Moment angulaire d’un point d’un solide en rotation autour d’un point O.
Soit un solide est animé d’un mouvement de rotation, de vecteur
vitesse angulaire 
 autour d’un point O. Le vecteur vitesse de chacun
de ses points Mi s’exprime à l’aide du produit vectoriel : 
.
Si l’on note mi la masse ponctuelle qui se trouve en Mi, celle-ci possède
un moment angulaire : 
or 
 (double produit)
3. Le produit mixte
Définition : Le produit mixte des trois vecteurs
wet , vu
est la valeur commune des trois produits
wvu 
,
uwv 
,
vuw .
il est noté :
wvu ,,
.
On démontre facilement, en utilisant les composantes des vecteurs
wet , vu
dans la base
,, kjiB
,
les égalités suivantes :
wvu 
=
vuw 
=
uwv 
D’après ce qui précède, on a les égalités suivantes :
122133113223321
,, wvwvuwvwvuwvwvuwvu 
vwuuwvwvu ,,,,,, 
Si
0,, wvu
, les trois vecteurs sont coplanaires.
IV. Dérivée d’une fonction
wet , vu

Cours de Mécanique, Pr M. ZOUNGRANA , UFR-SEA/U.O (first draft) Page 5
1. Fonction d’une seule variable
Une fonction f de la variable x est dérivable en x0, si le quotient 
 tend vers
une limite finie lorsque dx tend vers 0. Cette limite notée ′ est appelée dérivée de la fonction f
en x0.
Propriété utile : ′ est égale à la pente ou coefficient directeur de la tangente en x0 à la courbe
représentant .
Dérivées usuelles : - ′ ; ′
 ; ′;
- ′; ′
- ′′′; ′′′
2. Dérivée d’une fonction de fonction
Dans certaines situations, la variable d’une fonction peut, elle être fonction d’une autre variable :
Cas de l’énergie potentielle élastique d’un ressort . Dans cette fonction , la variable
position x, est elle-même une fonction de la variable temps t (x(t)).
La dérivée temporelle  de  s’écrit comme la limite lorsque dt tend vers 0 de :
En notant :  on a : 
 ′
Application :
⁃ Energie potentielle d’un ressort : 
  ′ 
⁃ Energie cinétique : 
3. Dérivées partielles
Elles concernent les fonctions de plusieurs variables f(x,y,z, t,..). Dans ce cas, lorsqu’on dérive la
fonction par rapport à une des variables, on considère que les autres variables restent constantes
Cas : déplacement vertical associé à la propagation d’une onde transversale dans une corde :
On définit ainsi les dérivées partielles :
 et 
En pratique, pour alléger la notation, on peut ne pas écrire l’indice repérant la ou les variables qui
rentent constantes.
 : 
 et 
V. Gradient
Soit  une fonction de trois variables. Lorsque x, y et z varient respectivement de dx,
dy et dz, conformément à ce qui précède, nous pouvons écrire que la fonction f varie de la quantité
df , appelée différentielle totale de la fonction f, et définie par :
.