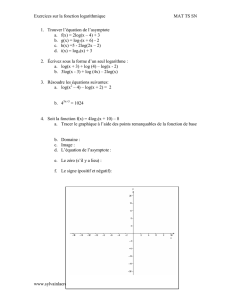
Les filtres actifs
1. Rôle des filtres
Le rôle principal des filtres en électronique et en traitement du signal est d’atténuer
certaines composantes d’un signal (partie inutile du signal) et de laisser passer d’autres (partie utile
du signal).
Plusieurs types de filtres existent, à titre d’exemple : les filtres passe-bas, passe-haut, passe
bande etc.
Les filtres peuvent être classés selon leurs natures (analogiques, numériques), selon leurs
composants (actifs, passifs) ou selon leurs degrés. Nous allons dans la suite de ce cours nous
intéresser aux filtres actifs (utilisant des composants actifs tels que les amplificateurs opérationnels
ou les transistors) de premier et de second ordre.
Dans une première partie nous allons expliquer la méthode de traçage des diagrammes de
Bode pour un système de premier et second ordre.
1. Méthode de traçage des diagrammes de Bode
Afin de tracer les diagrammes de Bode correspondants à une fonction de transfert , il
faut tout d’abord commencer par exprimer le gain F
db
, le gain en décibel, ainsi que le déphasage
en fonction de la fréquence ou de la pulsation avec :
Et
Une connaissance de quelques formules mathématiques est nécessaire pour faire ce calcul, à savoir :
Soit
un nombre complexe
Soit
!
deux nombres complexes
"
"
#
Soit !deux réels
$
%
#
&
'
Soient !
(
deux réels
)*
+
,
+
-
(
)*
+
.
+
-
(
/
Il faut par la suite calculer les limites particulières afin de déterminer les différentes
asymptotes du diagramme.

Le traçage se fait sur une échelle semi-log qui a l’avantage de compresser les données tout
en préservant la représentation des valeurs faibles.
Toute fonction 011 se représente sur un papier semi-log sous forme d’une droite.
2. Les filtres actifs de premier ordre
Les différents types de filtres peuvent être reconnus à partir de leur forme canonique. Nous
allons au cours de ce paragraphe citer les différentes formes des filtres de premier ordre ainsi qu’une
étude de leurs comportements vis-à-vis de la fréquence en traçant à chaque fois les diagrammes de
BODE correspondants.
2.1. Les filtres passe-bas
Comme son nom l’indique ce type de filtre laissera passer les signaux basses fréquences et
atténuer les signaux hautes fréquences. La forme générale de ce type de filtre est la suivante :
2
3
45
5-
ou encore
6
2+
-
+
-
37
Avec k un réel (positif ou négatif),
la pulsation et
(
la pulsation de coupure
Le traçage du diagramme de Bode permettra de mettre en évidence le type du filtre. Le
traçage se fera en appliquant les étapes du paragraphe 1.
Le calcul du gain en décibel ainsi que du déphasage donnent les résultats du tableau suivant :
Calcul du gain Calcul du déphasage
8
9
:
(
8
9
;:
(
;
9
<:$
(
%
9
#
:
=
:
(
>
9
#
:
(
si k>0
&'#$
+
+
-
%#
+
+
-
si k>0
&'?#$
+
+
-
%
L’étape suivante est donc de calculer les limites par rapport à la pulsation de coupure
(
:
Si
,
(
Si
(
Si
.
(
9
#
:
@A
:
99
C’est une asymptote horizontale
9
#
:
9
#
B
C
9
#
:
=
(
>
9#
(
#9
(
C’est une asymptote oblique de pente -20db
Pour la tracer on peut prendre deux valeurs
de
comme par exemple
(
et
:
(
Pour k>0
#
C’est une asymptote horizontale
#
:
#
?
D
#
/
#
?
C’ est une asymptote horizontale

Si
,
(
Si
(
Si
.
(
Pour k<0
?
#
?
C’est une asymptote horizontale
?
#
:
B
?
D
?
#
/
?
C’ est une asymptote horizontale
La figure suivante représente les diagrammes de Bode pour k>0 :
Exemples :
6
#
E
E
:
:
E
F6
6
:E
E
:
EF6
2.2. Filtres passe-haut
Les filtres passe-haut vont quant à eux laisser passer les hautes fréquences au dépend des basses
fréquences. Leur forme générale est la suivante :
9
G
5
5-
3G
5
5-
ou encore 69
7
+
-
37

Les diagrammes de Bode sont tracés de la même manière que celui du passe-bas :
Calcul du gain Calcul du déphasage
8
9
(
:
(
8
;
9
(
;
;:
(
;
9
(
<:$
(
%
9
(#:=:
(>
&
'
9
(
#:
(
si k>0
&'
H
#$
+
+
-
%
?
#
(
si k>0
&'?
H
#$
+
+
-
%
B?
#
(
Si
,
(
Si
(
Si
.
(
9
(
9
#
(
C’est une asymptote oblique de pente +20 db
Pour la tracer on peut prendre deux valeurs de
comme par exemple
(
et
:
(
9
#
:
9
#
B
C
9
(
#
:
9
9
C’est une asymptote horizontale
Pour k>0
?
#
?
C’est une asymptote horizontale
?
#
:
?
D
?
#
/
C’ est une asymptote horizontale
Pour k<0
B
?
C’est une asymptote horizontale
I
?
D
?
C’ est une asymptote horizontale
Les digrammes Bode correspondant à ce filtre passe-haut sont les suivants pour k>0 :

Exemples :
6#E
E
E
F6
:E
F6
6:E
E
EF6
:EF6
2.3. Filtre passe-tout ou déphaseur :
Un filtre passe tout a pour forme générale :
JKLM
N
OP
P-
3
OP
P-
ou encore JQM
NRS
3RS
Avec T
U
-
et VW:
Les calculs de gain et de déphasage donnent le tableau suivant :
 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
1
/
12
100%