Chapitre 1 Généralité sur la RDM

E.S.GE – SA 2022 Résistance des matériaux I BTS : Électromécanique
M.Chaambane Mohamed Chapitre 1 : Généralités sur la RdM
[e-mail] 1 | 8 P a g e
CHAPITRE 1 : GENEARALITE SUR LA RESISTANCE DES MATERIAUX
(RdM)

E.S.GE – SA 2022 Résistance des matériaux I BTS : Électromécanique
M.Chaambane Mohamed Chapitre 1 : Généralités sur la RdM
[e-mail] 2 | 8 P a g e
La résistance des matériaux, désignée souvent par la RDM, est la science du dimensionnement.
C’est une discipline importante de la mécanique, qui permet de concevoir une pièce ou tout un objet utilitaire, en outre
vérifier ça tenu contre les sollicitations et contraintes d’usage. Ce dimensionnement fait appel à des calculs qui prévoient
le comportement de l’objet dont la conception doit réunir les meilleures conditions de sécurité, d’économie et
d’esthétique.
1.1 Définitions et objectifs
Définitions
La résistance des matériaux est un modèle d’étude permettant de dimensionner les pièces afin :
 D’adapter le volume et la masse des mécanismes à leur résistance (par exemple un avion mal dimensionné en
résistance pourra se casser en vol, ou être trop lourd au contraire) ;
 D’adapter la déformation des pièces à l’application voulue (barre de torsion sur la direction assistée de voiture) ;
 D’avoir des pièces fusibles dans les mécanismes dont la limite de déformation élastique est parfaitement maîtrisée.
La résistance des matériaux doit nous permettre de comprendre les causes de défaillance des pièces et les anticiper.
D’autres modèles d’étude existent, permettant de dimensionner plus précisément les pièces comme la théorie de
l’élasticité des matériaux et des éléments finis. Cependant, la résistance des matériaux est un modèle très précis si
certaines conditions sont réunies.
Ces conditions sont appelées les hypothèses de la résistance des matériaux.
Objectif
La résistance des matériaux (RdM) étudie le comportement du solide déformable. Elle s’intéresse particulièrement au
calcul des dimensions des systèmes mécaniques pour qu’ils soient en mesure de supporter les efforts qui leur sont
appliqués pendant leur service dans les conditions de sécurité requise. Elle permet d’évaluer les efforts internes, les
contraintes ainsi que les déplacements et les rotations des structures.
1.2 Hypothèses générales
Ces hypothèses concernent essentiellement les matériaux utilisés, la forme des solides étudiés et le type d’action
mécanique exercée.
Hypothèses sur le matériau:
 L’homogénéité, l’isotropie et la continuité du matériau : On suppose que le matériau a les mêmes propriétés
élastiques en tous les points du corps, dans toutes les directions et que le matériau est assimilé à un milieu
continu (pas de défaut macroscopique tels que fissures, criques)
 L’élasticité et la linéarité du matériau : On suppose qu’en chaque point contraintes et déformation sont
proportionnelles et qu’près déformation, l’élément revient à son état initial.
Hypothèses sur les poutres
 Définition
Nous appelons poutre un solide dont une des dimensions est grande vis-à-vis de deux autres et qui est soumis à un
système de sollicitation qui le fait fléchir ou le déformer.
Une poutre est en général un solide engendré par une aire plane (S) dont le centre de gravité (G) décrit une courbe (C).
 Géométrie
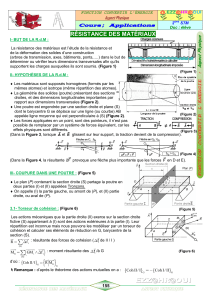
Les notions abordées dans ce chapitre ne sont valables que pour des solides ayant une forme de poutre (figure 1.1.),
c’est-à-dire un solide pour lequel :
- Il existe une ligne moyenne lm, continue, passant par les centres de gravité des sections du solide ;
- La longueur L est supérieure ou égale à 5 fois le diamètre D ;
- Le solide admet un seul et même plan de symétrie pour le chargement et la géométrie.
Remarques :
- L’aire de la section (S) est appelée section droite ou section normale de la poutre

E.S.GE – SA 2022 Résistance des matériaux I BTS : Électromécanique
M.Chaambane Mohamed Chapitre 1 : Généralités sur la RdM
[e-mail] 3 | 8 P a g e
- La courbe (C) est appelée fibre moyenne de la poutre, si la fibre moyenne est une droite, la poutre est dite droite.
- Le rayon de courbure de la fibre moyenne est suffisamment grand par rapport à la dimension transversale de la
poutre.
Figure 1.1 : Elément d’une poutre
Hypothèses sur les efforts extérieurs :
 Toute action mécanique est représentée par un torseur en un point. Ces actions peuvent être concentrées ou
réparties, exercées à distance ou en contact.
 Les efforts extérieurs sont situés dans le plan de symétrie de la poutre ou disposés symétriquement par
rapport à ce plan.
Domaine de validité de la résistance des matériaux :
 Hypothèse des petites déformations : Les déformations dues aux charges sont négligeables par rapport
aux dimensions des composants étudiés.
 Hypothèse de Navier-Bernoulli (hypothèse des sections planes) : les sections droites restent planes et
normales à la fibre moyenne au cours de la déformation.
 Hypothèse de Saint Venant : Les contraintes (et par suite les déformations qui leur sont liées par la loi de
Hooke), dans une région éloignée des points d’application d’un système de forces, ne dépendent que de la
résultante générale et du moment résultant de ce système de forces.
Ces hypothèses simplificatrices conduisent à des solutions approchées qui permettent en général une bonne
approximation du comportement des structures soumises à différents types de charges.
1.3 Les réactions d’appuis
Un appui est un élément extérieur en contact avec la structure étudiée et la réaction d’appui dépend de la nature de la
liaison appui-structure. Une structure est reliée au monde extérieur par un certain nombre de liaisons. Ces liaisons dans
le plan sont de 3 sortes :
Liaison appui-simple (ou sphère cylindre)
Cette liaison est fréquente puisqu'elle est réalisée par exemple à partir d'un roulement à une rangée de billes non bloqué
axialement. Un appui simple sert alors à bloquer un seul déplacement qui se trouve en direction perpendiculaire à la
A
G
B
L
D
d
Plan de symétrie de la poutre
Ligne moyenne Lm
Section droite
(S)

E.S.GE – SA 2022 Résistance des matériaux I BTS : Électromécanique
M.Chaambane Mohamed Chapitre 1 : Généralités sur la RdM
[e-mail] 4 | 8 P a g e
droite joignant les points de contact. L’appui simple introduit une seule inconnue dans l’étude de la poutre.
Figure 1.2 : Liaison appui – simple
Liaison rotule (appui ou articulation)
Il s’agit d’une liaison rotule considérée dans un plan qui est le plan moyen de la poutre.
Elle peut correspondre à la liaison de la poutre avec un roulement à une rangée de billes muni de ses arrêts axiaux
(éventuellement elle est susceptible de représenter aussi un appui simple).
L’articulation introduit deux inconnues, par projection sur deux directions du plan moyen.
Figure 1.3 : Caractéristiques d’une liaison rotule dans le plan
Liaison d’encastrement
Il s’agit d’une liaison complète considérée dans un plan qui est le plan moyen de la poutre. Cette liaison reliant la poutre
à une pièce considérée comme fixe, on représente une liaison encastrement par le symbole de la masse.
Ce type d’appui introduit donc 3 inconnues, les deux projections de R sur deux axes du plan moyen et l’intensité du
Moment M perpendiculaire au plan moyen.
Figure 1.4 : Caractéristiques d’une liaison d’encastrement dans le plan
Remarques :
En théorie des poutres, on distingue en général deux types de charges :
 Les charges concentrées qui s'appliquent en un point de la poutre et définie par un torseur en ce point
d'application. Si ce torseur se réduit à une résultante, on l'appelle force concentrée. Si ce torseur se réduit à un
couple (ou un moment) on l'appelle moment concentré.
 Les charges réparties qui sont distribuées continûment le long d'un segment de la poutre et sont représentées
par un champs de vecteurs uniforme ou non.
A
Le torseur des actions transmissibles au niveau d’un
appui simple s’écrit :
Le torseur des petits déplacements au niveau du point A, maintient trois paramètres non nuls,
, cependant l’action  impose un déplacement v nul en A : , appui simple.
A
Le torseur des actions transmissibles au niveau d’un appui simple s’écrit :
Le torseur des petits déplacements au niveau du point A, maintient deux paramètres non
nuls,   , cependant les actions  et  imposent des déplacement u et v nul en A :
, articulation
A
Le torseur des actions transmissibles au niveau d’un appui simple s’écrit :
L’ensemble des trois actions de ce torseur imposent des déplacements nuls
en A : 

E.S.GE – SA 2022 Résistance des matériaux I BTS : Électromécanique
M.Chaambane Mohamed Chapitre 1 : Généralités sur la RdM
[e-mail] 5 | 8 P a g e
1.4 Torseur de cohésion
Les efforts intérieurs ou de cohésion sont les efforts qui agissent à l’intérieur des poutres et qui assurent l’équilibre ou
la cohésion de la structure sous l’action des charges extérieures exercées. La connaissance de ces efforts de cohésion
nous renseignera sur l’état de sollicitation de la poutre étudiée, et permettra d’évaluer sa résistance aux efforts qui lui
sont appliqués.
Expression du torseur des efforts intérieurs
Soit une poutre (E) équilibre sous l'effet d'actions mécaniques extérieures. Pour me en évidence les efforts transmis au
niveau d'une section, nous effectuons une coupure imaginaire dans le plan P contenant S. Il la sépare en deux tronçons
 (Partie gauche) et  (Partie droite) (voir Figure 1.3).
Figure 1.5 : Coupe fictive sur une poutre
On isole le tronçons E1 :
Les actions mécaniques que le tronçon E2 exerce sur le tronçon E1 à travers la section S sont des actions mécaniques
intérieures à la poutre E. Nous ignorons à priori la nature, cependant la liaison entre E1 et E2 peut être modélisée par
une liaison complète. On peut donc modéliser l’action mécanique E2 sur E1 par un torseur appelé torseur de cohésion
et noté  dont les éléments de réductions en G seront  et .
L’équilibre du tronçon 1 ou de la partie gauche se traduit par : 
Avec  
E1
E2
(S)
A
G
B
x
E1
(S)
A
G
x
Tronçons AG :