CHIMIE
Exercice 1 :
Exercice 2 :
PHYSIQUE
Exercice 1 :
Un point matériel (S) se déplace le long d’un axe horizontal (x’Ox). Sa position M est repérée à
chaque instant, par son abscisse () = OM dans un repère (0,⃗) : où O correspond à la position de (S)
lorsqu’il est au repos et
⃗
est un vecteur unitaire porté par l’axe (x’Ox).
A un instant de date t = 0, un dispositif d’acquisition approprié est mis en marche permettant
d’enregistrer l’évolution de son élongation () au cours du temps. On obtient alors la courbe ci-
contre :
Prof : Smaali Faouzi Devoir de Synthèse n°2 3
ème
Sc
1/2

1) Préciser la nature du mouvement du point matériel (S) ? Justifier la réponse.
2) Déterminer, à partir de la courbe :
a) l’élongation maximale Xmax
b) la valeur de la période T et celle de la fréquence N du mouvement de (S).
3) L’équation horaire du mouvement du point matériel (S) est de la forme :
x(t) = Xmax sin ( ω t + φx )
a) Déterminer la valeur de la phase initiale φx et celle de la pulsation ω
b) Ecrire l’expression de la vitesse instantanée v (t) du point matériel (S) sous la forme :
v(t) = Vmax sin (ω t + φv)
On précisera la valeur numérique de chacune des grandeurs Vmax et φv
c) Représenter sur votre copie la courbe v(t).
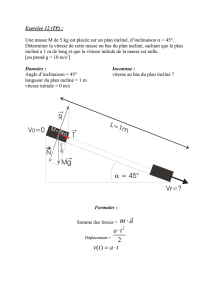
Exercice 2 :
I ) Au sommet B d’un plan AB incliné sur l’horizontale d’un angle de sinus égale à 0,1 . On
abandonne sans vitesse initiale un solide ponctuel (S) de masse m =200 g . La distance AB = 2 m
1) En négligeant les frottements sur le plan incliné AB , déterminer :
a) La nature du mouvement entre B et A
b) Le temps mis sur le plan incliné
c) La valeur de la vitesse VA en arrivant au bas du plan
2) La détermination expérimentale du temps mis de B à A donne la valeur t’ = 2,5 s
Déduire l’existence de forces des frottements f . Calculer la valeur de f
II ) Le solide (S) est maintenant lancé en O sur le plan horizontale OA , avec une vitesse initiale V0 de
valeur 2 m.s-1
1) En supposant le plan OA parfaitement lisse , trouver la valeur de la vitesse d’arrivée en A
2) Le solide gravit ensuite le plan incliné AB sur lequel la force de frottement vaut 0,072 N
a) Préciser la position du point C où le solide rebrousse chemin
b) Quel temps met-il pour effectuer le trajet ACA ? on donne : g = 10 m.s-2
2/2
1
/
2
100%