Opérateur laplacien — Wikipédia

Opérateur laplacien
Opérateur différentiel, qui, appliqué à un
champ scalaire, exprime les variations
dynamiques dans l'espace de ce champ
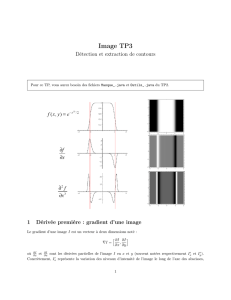
L'opérateur laplacien, ou simplement le laplacien, est l'opérateur différentiel défini par
l'application de l'opérateur gradient suivie de l'application de l'opérateur divergence:
Intuitivement, il combine et relie la description statique d'un champ (décrit par son gradient)
aux effets dynamiques (la divergence) de ce champ dans l'espace et le temps. C'est
l'exemple le plus simple et le plus répandu d'opérateur elliptique.
Il apparaît dans la formulation mathématique de nombreuses disciplines théoriques, comme
la géophysique, l'électrostatique, la thermodynamique, la mécanique classique et quantique.
On le retrouve systématiquement dans les expressions de l'équation de Laplace, de l'équation
de Poisson, de l'équation de la chaleur et l'équation d'onde.
L'opérateur laplacien appliqué deux fois est appelé bilaplacien.
Effet physique
Une manière d'aborder la compréhension du laplacien est de remarquer qu'il représente
l'extension en dimension trois (ou deux, ou plus) de ce qu'est la dérivée seconde en
Présentation

dimension un.
De même que le gradient est l'équivalent en 3D de la variation temporelle, de même le
laplacien reflète la dérivée seconde qu'est l'accélération: il prend des valeurs importantes
dans des zones qui sont fortement concaves ou convexes, c'est-à-dire qui marquent un
déficit par rapport au plan de «distribution moyenne» que matérialise le gradient. Une valeur
importante (en positif ou négatif) du laplacien signifie que localement, la valeur du champ
scalaire est assez différente de la moyenne de son environnement; et sur le plan dynamique,
cette différence de valeur demande à être comblée.
D'une manière générale, on aura donc des équations physiques traduisant que la vitesse
d'évolution d'une grandeur physique en un point sera d'autant plus grande que le laplacien est
important en ce point, le rapport entre les deux étant donné par un coefficient de diffusion.
C'est ce que traduit par exemple l'équation de la chaleur:
= .
La vitesse de variation de la température en un point est (à un coefficient près) d'autant plus
grande que l'écart de température avec la moyenne de son entourage est important.
Définition
Symbolisé par la lettre grecque delta, il correspond donc à l'opérateur nabla appliqué deux
fois à la fonction considérée. Il s'applique le plus souvent aux champs scalaires, et son
résultat est alors également un champ scalaire. La première application de nabla porte sur
un scalaire: il s'agit donc d'un gradient, et le résultat est un vecteur:
La deuxième opération porte alors sur un vecteur. Il s'agit alors d'une divergence, et le
résultat est un scalaire:
,
d'où les identités mentionnées en introduction.

Étant le résultat d'une double dérivation spatiale, s'il est appliqué à une grandeur physique G
de dimension [G], le résultat sera en [G] par mètre carré.
Changement de système de coordonnées
Pour un champ scalaire, une fois établi le tenseur métrique g, on a:
.
Cette formule permet de calculer facilement le laplacien dans un système de coordonnées
quelconque.
Laplacien de tenseurs
De manière plus générale, l'opérateur laplacien vectoriel, lui, s'applique aux champs
vectoriels, et la définition du laplacien par la divergence du gradient (celle-ci étant prise sur
l'indice tensoriel créé par le gradient) est valable pour un champ tensoriel quelconque a.
Attention cependant à ce que dans ce cas, la formule devient fausse. Le
laplacien d'une matrice de coordonnées est la matrice des laplacien des coordonnées. Le
laplacien
a le même nombre d'indices que a. Le laplacien admet une généralisation aux espaces non
euclidiens suffisamment lisses, appelé opérateur de Laplace-Beltrami.
Coordonnées cartésiennes
En coordonnées cartésiennes bidimensionnelles, le laplacien est:
.
En coordonnées cartésiennes tridimensionnelles:
.
En coordonnées cartésiennes dans ℝn:
Expression dans différents systèmes de coordonnées

.
Coordonnées polaires
En coordonnées polaires (donc en dimension 2), le laplacien s'exprime de la façon
suivante[1],[2]:
Coordonnées cylindriques (dimension 3)
Il suffit d'ajouter au laplacien en coordonnées polaires ci-dessus pour obtenir celui
correspondant au paramétrage cylindrique :
Coordonnées sphériques (dimension 3)
Avec le paramétrage
,
le laplacien s'exprime de la façon suivante[3]:
.
Ou sous une autre forme, qui peut être plus adaptée pour certains calculs, et redonne la
formule précédente une fois développée:
.
Coordonnées hypersphériques (dimension 4)
Avec le paramétrage

,
le laplacien s'exprime de la façon suivante[4]:
.
Coordonnées sphériques en dimension quelconque
En coordonnées hypersphériques
,
le laplacien s'exprime de la façon suivante[5]:
.
L'opérateur laplacien est linéaire:
L'opérateur laplacien vérifie la règle de Leibniz pour un opérateur différentiel d'ordre deux:
L'opérateur laplacien est un opérateur négatif, au sens où, pour toute fonction lisse ϕ à
support compact, on a:
.
Cette égalité se démontre en utilisant la relation , en intégrant par parties,
et en utilisant une version du théorème de Stokes, qui se transpose à l'intégration par
parties dans le cas unidimensionnel.
L'opérateur laplacien est indépendant du choix de la base orthonormale décrivant les
variables spatiales[6].
Article détaillé: Fonction harmonique.
Propriétés
Fonction harmonique