Image TP3

Image TP3
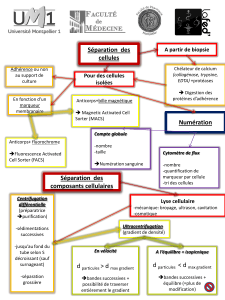
Détection et extraction de contours
Pour ce TP, vous aurez besoin des fichiers Masque_.java et Outils_.java du TP2.
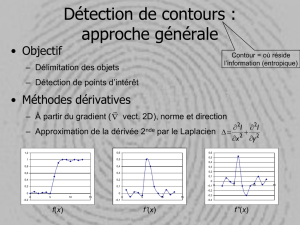
1 Dérivée première : gradient d’une image
Le gradient d’une image Iest un vecteur à deux dimensions noté :
∇I=h∂I
∂x ,∂I ∂y i
où ∂I
∂x et ∂I ∂u sont les dérivées partielles de l’image Ien xet y(souvent notées respectivement I0
xet I0 y).
Concrètement, I0
xreprésente la variation des niveaux d’intensité de l’image le long de l’axe des abscisses,
1

et I0
yle long de l’axe des ordonnées. Ainsi, les points maxima des dérivées partielles caractérisent de fortes
variations des niveaux d’intensité, et peuvent donc être interprétés comme les contours de l’image.
En pratique, il n’est pas possible de calculer véritablement les dérivées partielles d’une image car il ne s’agit
pas d’une fonction continue : l’image est de taille finie et discrétisée selon une grille de pixels. Il est cependant
possible d’approximer « convenablement » les dérivées partielles de la manière suivante :
I0
x(x, y)≈I(x+ 1, y)−I(x, y)
1≈I(x, y)−I(x−1, y) 1.
Cette opération ressemble beaucoup au type d’opérations effectuées lors de l’application d’un filtre de convo-
lution (la nouvelle valeur d’un pixel est une fonction de son voisinage). Ceci suggère d’approximer le gradient
d’une image à l’aide de filtres de convolution. En particulier, on notera le filtre de Sobel défini comme suit :
I0
x=I∗
−101
−202
−101
et I0
y=I∗
−1−2−1
000
121
.
Une fois que les deux composantes du gradient ont été calculées, il est possible de calculer la norme du
gradient (qI0
x
2+I0
y
2) ainsi que son orientation (atan2(I0
x, I0 y)).
Les plugins « SobelX » et « SobelY » sont déjà codés et affichent les deux composantes du gradient
(ramenées dans l’espace des niveaux de gris). Testez-les sur différentes images.
Dans le fichier Sobel_.java, complétez le code de la méthode run(...) afin de calculer la norme du
gradient d’une image. Vous testerez votre plugin sur différentes images. Que se passe-t-il lorsque l’image
d’origine est bruitée ?
Application à l’extraction de contours
Nous voulons développer un filtre qui affichera les contours en blanc et le reste en noir. Nous avons vu que le
bruit présent dans l’image introduit de « faux contours ». L’algorithme sera donc constitué de trois étapes :
1. Élimination du bruit par un filtre gaussien ;
2. Détection des contours par gradient de Sobel ;
3. Seuillage de l’image résultante.
Dans le fichier ExtractionContours_.java, complétez le code de la méthode run(...) en suivant les
consignes indiquées en commentaire. Vous testerez votre plugin avec différents paramètres.
2 Dérivée seconde : laplacien d’une image
Le laplacien d’une image est défini comme suit :
∆I(x, y) = ∇2I(x, y) = ∂2I
∂x2(x, y) + ∂2I ∂x2(x, y).
2

Remarque : contrairement au gradient qui était un vecteur, il s’agit ici d’un nombre scalaire.
Dans le domaine discret, le laplacien peut être obtenu de manière similaire au gradient, par convolution avec
un masque bien choisi. Les masques suivants peuvent être choisis :
L4=
010
1−4 1
010
ou L8=
111
1−8 1
111
Les plugins Laplace4 et Laplace8 sont déjà codés et affichent le laplacien d’une image (ramené dans
l’espace des niveaux de gris). Testez-les sur différentes images. Comment sont caractérisés les contours ?
Application au réhaussement de contours
Dans le fichier Rehaussement_.java, complétez le code de la méthode run(...) en suivant les consignes
indiquées en commentaire. Testez le plugin sur différentes images.
3