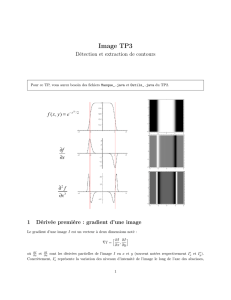
Opérateur laplacien Opérateur différentiel, qui, appliqué à un champ scalaire, exprime les variations dynamiques dans l'espace de ce champ L'opérateur laplacien, ou simplement le laplacien, est l'opérateur différentiel défini par l'application de l'opérateur gradient suivie de l'application de l'opérateur divergence : Intuitivement, il combine et relie la description statique d'un champ (décrit par son gradient) aux effets dynamiques (la divergence) de ce champ dans l'espace et le temps. C'est l'exemple le plus simple et le plus répandu d'opérateur elliptique. Il apparaît dans la formulation mathématique de nombreuses disciplines théoriques, comme la géophysique, l'électrostatique, la thermodynamique, la mécanique classique et quantique. On le retrouve systématiquement dans les expressions de l'équation de Laplace, de l'équation de Poisson, de l'équation de la chaleur et l'équation d'onde. L'opérateur laplacien appliqué deux fois est appelé bilaplacien. Présentation Effet physique Une manière d'aborder la compréhension du laplacien est de remarquer qu'il représente l'extension en dimension trois (ou deux, ou plus) de ce qu'est la dérivée seconde en dimension un. De même que le gradient est l'équivalent en 3D de la variation temporelle, de même le laplacien reflète la dérivée seconde qu'est l'accélération : il prend des valeurs importantes dans des zones qui sont fortement concaves ou convexes, c'est-à-dire qui marquent un déficit par rapport au plan de « distribution moyenne » que matérialise le gradient. Une valeur importante (en positif ou négatif) du laplacien signifie que localement, la valeur du champ scalaire est assez différente de la moyenne de son environnement ; et sur le plan dynamique, cette différence de valeur demande à être comblée. D'une manière générale, on aura donc des équations physiques traduisant que la vitesse d'évolution d'une grandeur physique en un point sera d'autant plus grande que le laplacien est important en ce point, le rapport entre les deux étant donné par un coefficient de diffusion. C'est ce que traduit par exemple l'équation de la chaleur : = . La vitesse de variation de la température en un point est (à un coefficient près) d'autant plus grande que l'écart de température avec la moyenne de son entourage est important. Définition Symbolisé par la lettre grecque delta, il correspond donc à l'opérateur nabla appliqué deux fois à la fonction considérée. Il s'applique le plus souvent aux champs scalaires, et son résultat est alors également un champ scalaire. La première application de nabla porte sur un scalaire : il s'agit donc d'un gradient, et le résultat est un vecteur : La deuxième opération porte alors sur un vecteur. Il s'agit alors d'une divergence, et le résultat est un scalaire : , d'où les identités mentionnées en introduction. Étant le résultat d'une double dérivation spatiale, s'il est appliqué à une grandeur physique G de dimension [G], le résultat sera en [G] par mètre carré. Changement de système de coordonnées Pour un champ scalaire, une fois établi le tenseur métrique g, on a : . Cette formule permet de calculer facilement le laplacien dans un système de coordonnées quelconque. Laplacien de tenseurs De manière plus générale, l'opérateur laplacien vectoriel, lui, s'applique aux champs vectoriels, et la définition du laplacien par la divergence du gradient (celle-ci étant prise sur l'indice tensoriel créé par le gradient) est valable pour un champ tensoriel quelconque a. Attention cependant à ce que dans ce cas, la formule devient fausse. Le laplacien d'une matrice de coordonnées est la matrice des laplacien des coordonnées. Le laplacien a le même nombre d'indices que a. Le laplacien admet une généralisation aux espaces non euclidiens suffisamment lisses, appelé opérateur de Laplace-Beltrami. Expression dans différents systèmes de coordonnées Coordonnées cartésiennes En coordonnées cartésiennes bidimensionnelles, le laplacien est : . En coordonnées cartésiennes tridimensionnelles : . En coordonnées cartésiennes dans ℝn : . Coordonnées polaires En coordonnées polaires (donc en dimension 2), le laplacien s'exprime de la façon suivante[1],[2] : Coordonnées cylindriques (dimension 3) Il suffit d'ajouter au laplacien en coordonnées polaires ci-dessus pour obtenir celui correspondant au paramétrage cylindrique : Coordonnées sphériques (dimension 3) Avec le paramétrage , le laplacien s'exprime de la façon suivante[3] : . Ou sous une autre forme, qui peut être plus adaptée pour certains calculs, et redonne la formule précédente une fois développée : . Coordonnées hypersphériques (dimension 4) Avec le paramétrage , le laplacien s'exprime de la façon suivante[4] : . Coordonnées sphériques en dimension quelconque En coordonnées hypersphériques , le laplacien s'exprime de la façon suivante[5] : . Propriétés L'opérateur laplacien est linéaire : L'opérateur laplacien vérifie la règle de Leibniz pour un opérateur différentiel d'ordre deux : L'opérateur laplacien est un opérateur négatif, au sens où, pour toute fonction lisse ϕ à support compact, on a : . Cette égalité se démontre en utilisant la relation , en intégrant par parties, et en utilisant une version du théorème de Stokes, qui se transpose à l'intégration par parties dans le cas unidimensionnel. L'opérateur laplacien est indépendant du choix de la base orthonormale décrivant les variables spatiales[6]. Fonction harmonique Article détaillé : Fonction harmonique. Une fonction (avec ) est dite harmonique si elle vérifie l'équation suivante, appelée équation de Laplace : . Interprétation Article connexe : Laplacien discret. Le raisonnement se limitera au cas du plan. La dérivée d'une fonction en un point situé sur une droite se définit comme la limite du rapport des variations autour de ce point de la fonction et de la variable lorsque cette dernière variation tend vers zéro. En calcul numérique, une approximation de cette dérivée est donc obtenue pour un pas h en utilisant des différences finies : . La dérivée seconde s'exprime par . Cette quantité, qui tend vers le laplacien lorsque h tend vers 0, est proportionnelle à la différence entre la demi-somme des valeurs extrêmes et la valeur centrale. La propriété se généralise à un nombre quelconque de variables. Approche géométrique Il est indispensable de bien dégager une interprétation physique simple pour le laplacien, autrement dit de se demander quelle est la signification physique de la quantité ∇2ϕ, où ϕ est une grandeur physique quelconque. En particulier, ϕ peut être le potentiel gravifique V ou le potentiel de pesanteur U, mais ϕ peut aussi désigner une quantité plus compliquée qu'une simple grandeur scalaire, par exemple un vecteur ou un tenseur. Le laplacien étant un opérateur scalaire, on peut donc établir sa signification physique dans un système de coordonnées au choix. Pour des raisons de simplicité, nous utilisons ici des coordonnées cartésiennes Ox, Oy, Oz, dans lesquelles ∇2 s'exprime par . Supposons qu'en un point O quelconque, pris comme origine de ce système d'axes Oxyz, le champ ϕ prenne la valeur ϕ0. Considérons un cube élémentaire de côté a, dont les arêtes sont parallèles aux axes de coordonnées et dont le centre se confond avec l'origine O. La valeur moyenne de ϕ dans ce cube élémentaire, autrement dit la valeur moyenne de ϕ au voisinage du point O, est fournie par l'expression , où les trois intégrations portent chacune sur le cube C = [−a⁄2, a⁄2]3. En un point P(x, y, z) arbitraire au voisinage de O(0,0,0), développons ϕ en série de TaylorMaclaurin. On a ainsi : D'une part, les fonctions impaires dans cette expression fournissent, par intégration de −a⁄2 à a⁄2, une contribution nulle à ϕ. Par exemple, . D'autre part, les fonctions paires fournissent chacune une contribution de a5/12. Par exemple, . On en déduit que , ou encore . Comme le point O a été choisi arbitrairement, on peut l'assimiler au point courant P et laisser tomber l'indice 0. On obtient donc l'expression suivante, dont l'interprétation est immédiate : , c'est-à-dire la quantité ∇2ϕ est proportionnelle à la différence ϕ – ϕ. La constante de proportionnalité vaut 24/a2 en axes cartésiens. En d'autres termes, la quantité ∇2ϕ est une mesure de la différence entre la valeur de ϕ en un point quelconque P et la valeur moyenne ϕ au voisinage du point P. En particulier, les fonctions harmoniques (voir supra) ont la propriété d'être des fonctions moyennes (ou des « fonctions de classe moyenne »). Remarque : le laplacien d'une fonction peut aussi être interprété comme la courbure moyenne locale de la fonction, que l'on visualise aisément pour une fonction f à une seule variable. On vérifiera aisément que le raisonnement proposé ici pour le laplacien s'applique à une fonction f et à sa dérivée seconde. La dérivée seconde (ou courbure) représente ainsi la déviation locale de la moyenne par rapport à la valeur au point considéré. Notes et références 1. Expression du laplacien en coordonnées polaires (dimension 2) (http://www.cafepedagog ique.net/communautes/MarcCourbot/Documents/TRAVAUX%20SUR%20LE%20LAPLACI EN/2D%20-%20LAPLACIEN.pdf) . 2. Calcul différentiel/Exercices/Différentiabilité#Exercice 7 (https://fr.wikiversity.org/wiki/fr: Calcul_diff%C3%A9rentiel/Exercices/Diff%C3%A9rentiabilit%C3%A9#Exercice_7) sur Wikiversité. 3. Expression du laplacien en coordonnées sphériques (dimension 3) (http://www.cafepeda gogique.net/communautes/MarcCourbot/Documents/TRAVAUX%20SUR%20LE%20LAPL ACIEN/3D%20-%20LAPLACIEN.pdf) . 4. Expression du laplacien en coordonnées hypersphériques (dimension 4) (http://www.cafe pedagogique.net/communautes/MarcCourbot/Documents/TRAVAUX%20SUR%20LE%20L APLACIEN/4D%20-%20LAPLACIEN.pdf) . 5. Expression du laplacien en coordonnées sphériques (dimension quelconque) (http://www. cafepedagogique.net/communautes/MarcCourbot/Documents/TRAVAUX%20SUR%20L E%20LAPLACIEN/-%20LAPLACIEN%20(%20dimension%20n%20)%20-.pdf) . 6. On le montre en utilisant le fait que la transposée de la matrice de passage d'une base à l'autre est identique à son inverse. Voir aussi Articles connexes Harmonique cylindrique Harmonique sphérique Théorie du potentiel Liens externes (en) Eric W. Weisstein, « Laplacian » (http://mathworld.wolfram.com/Laplacian.html) , sur MathWorld (en) Milton Abramowitz et Irene Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables [détail de l’édition] (lire en ligne (http://people. math.sfu.ca/~cbm/aands/) ), chap. 21 (http://people.math.sfu.ca/~cbm/aands/page_75 1.htm) Portail de l'analyse Portail de la physique Portail de la géodésie et de la géophysique Ce document provient de « https://fr.wikipedia.org/w/index.php? title=Opérateur_laplacien&oldid=168222259 ». Dernière modification il y a 2 ans par 2A02:120B:C3CE:69B0:F588:DDDE:EEAF:3B8 Wikipédia Le contenu est disponible sous licence CC BY-SA 3.0 sauf mention contraire.