BTS CRSA 1ère année - Sciences physiques et chimiques appliquées
TD du chapitre 3 : Dynamique des fluides
Exercice n°1 : vitesse d’écoulement-débit masse- débit volume
1. Dans un tube de diamètre 12,7mm, s’écoule à la vitesse 1,2 m.s-1 de l’huile de masse volumique
820kg.m-3. Calculer le débit volumique puis le débit massique.
2. On veut injecter 3,82cm3 de polyéthylène de masse volumique ρ=920 kg.m-3 dans un moule. La
vitesse d’injection à l’entrée du moule est de v=2,1m.s-1 dans une buse de diamètre 3mm.
2.1 Calculer le débit volumique d’injection.
2.2 En déduire la durée d’injection pour le volume considérée.
Exercice n°2 :

Exercice n°3 : Turbine
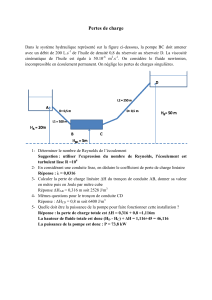
Une turbine est alimentée par une retenue d'eau selon le schéma ci-dessous.
On donne :
Diamètre
d
de la conduite d'alimentation et de déversoir :
d
= 700 mm
Pression aux points A, C et D : pA = pD =1,01 bar pC = 1, 1 bar
Cote des points A, B et C : zA = 363 m zB = 361 m zC = 353 m
L'eau sera considérée comme un fluide parfait incompressible et on supposera que le niveau de l'eau
dans la retenue est constant.
1. Calculer, dans ces hypothèses, la vitesse d'écoulement vC du fluide au point C (c'est-à-dire à l'entrée
de la turbine).
2. En déduire le débit-volume qv de l'eau dans la conduite.
3. Justifier que les vitesses d'écoulement en B et en C sont égales.
4. Calculer la pression pB à l'entrée de la conduite.
5. Calculer la puissance fournie par l'eau à la turbine.
Exercice n°4 : Alimentation en eau potable d’un phare maritime
On s’intéresse au circuit d’alimentation en eau potable d’une tour maritime de 45m de hauteur. Le
circuit est schématisé ci-dessous :
Les pressions A et B sont supposées égales à la
pression atmosphérique.
On donne :
Masse volumique de l’eau : ρ=1000kg.m-3
Accélération de pesanteur : g=9,81m.s-2
Diamètre de la canalisation :D=2,7cm
Débit volumique : qV=3,5.10-4 m3.s-1
Patm=1.105 Pa
1. On veut remplir un récipient de 20L, situé en B. Combien de temps faut-il pour le remplir ?
Données :
ρeau=1000kg.m-3
g=10m.s-2

2. Calculer la vitesse d’écoulement dans la canalisation
3. Calculer la pression E à l’entrée de la pompe en utilisant la relation de Bernoulli, les pertes en charge
entre A et E valant Δp1=1000Pa
4. Pour éviter les problèmes de cavitation (vaporisation du liquide dans la canalisation très
dommageable pour la pompe) la pression de l’eau doit être dans le cas étudié supérieure à p=1700Pa
à l’entrée de la pompe. Risque-t-on un problème de cavitation ?
5. Les pertes en charge sur l’ensemble du circuit sont estimées à Δp2=6500Pa. Calculer la puissance
hydraulique Ph de la pompe.
Exercice n°5 :
Une pompe hydraulique a un débit de 45 L/min. La pression
p
1 à la sortie de la pompe est de 80 bar. L’axe
du flexible de refoulement est horizontal et son diamètre est de 15 mm.
1. Calculer la vitesse
v
1 d’écoulement du fluide à la sortie de la
pompe
2. En raison d’une fausse manœuvre, le flexible situé à la même
hauteur que la pompe subit une brusque rupture. Le fluide passe
brusquement d’une pression de 80 bar et d’une vitesse d’écoulement
de 4 m/s à une pression
p
2 égale à celle de la pression
atmosphérique et à une vitesse
v
2. Calculer, arrondie à 1 m/s, la
vitesse
v
2 d’expulsion du fluide.
Données numériques :
1 bar = 105 Pa
pression atmosphérique : 1 bar
masse volumique du fluide : ρ = 800 kg/m3.
Exercice n°6 :
On considère un réservoir remplie d’eau à une hauteur H= 3 m ,
muni d’un petit orifice à sa base de diamètre d= 10 mm très
petit devant de diamètre du réservoir.
1. En précisant les hypothèses prises en comptes, appliquer le
théorème de Bernoulli pour calculer la vitesse v2 d’écoulement
d’eau.
2. En déduire le débit volumique Qv en (l/s) en sortie de
l’orifice.
Donnée : g=9,81 m/s2.
Eléments de réponses:
Ex1 : 1. 1 ,52.10-4 m3.s-1 ; 0,124 kg.s-1 2.1 1,48.10-5 m3.s-1 2.2 0,258 s
Ex2 : 1 3969 Pa 2.1 0,081 kg.m-3 2.2 0,375 m.s-1
Ex3 : 1 13,3m.s-1 2 5,12m3.s-1 4 30720 Pa 5 -46,3kW
Ex4 : 1. 57,1s 2. 0,611s 3. 49 950 Pa
5. 122W
Ex5 : 1. 4,26m.s-1 2. 141 m.s-1
Ex6 : 1. 7,67m.s-1 2. 6.02.10-4 m3/s
1
/
3
100%