exercices-solutions

Exercices
Asservissement & Régulation Page: 56 Propose par: SOYED-Abdessamï
Exercices
Exercice 1:
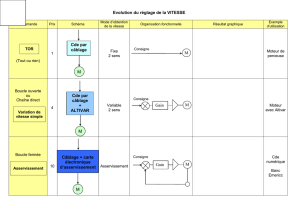
Soit un systéme asservi représenté par le schéma ci-dessous.
1. Simplifier le schéma blocs ci-dessus,
2. En déduire la fonction de transfert
S(p)
H(p)=
E(p)
, en fonction de H1(p) et H2(p),
3. Soit 1
1
H (p)=
p+1
et 2
1
H (p)=
p
, déterminer l’expression de H(p).
Par la suite on prend 21 H(p)=
p +3p+2
.
Le systeme est successivement excité par un échelone =(t)
u(t)
et une rampee =t(t)
.u(t)
.
4. Détreminer les expresions 1
S (p)
et 2
S (p)
, pour les deux entrées,
5. En déduire leurs valeurs initiales finales,
6. Détreminer les expressions de s1(t) et s2(t), pour les deux entrées,
7. Détreminer le module et l’argument de H(jw).
(p)H1
E(p) S(p)
2
H (p)

Exercices
Asservissement & Régulation Page: 57 Propose par: SOYED-Abdessamï
Exercice 2:
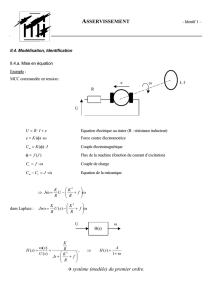
Soit un circuit électrique régit par l’équation différentielle suivante: di 1
Ri+L + idt=e(t)
dt C
.
On suppose que toutes les conditions intiales sont nulles, et on pose:
2
0
1
LC=
w
et
R C
m=
2 L
.
On prend e(t) =10.u(t).
1. Détreminer l’expression du courant I(p), en fonction de (m, R et w0),
2. Pour m =1, R =1 et w0 =1rad/s, en déduire i(0) et i(+),
3. Détreminer l’expression temporelle du courant i(t), et la réprésenter,
4. En deduire le temps et le courant maximum correspondant.
Exercice 3:
1. Trouver la transformée de Laplace des fonctions suivantes, en déduire leurs expressions
temporelles.
f(t)
T
t
E
0
E
t
g(t)
T
0
0
E
t
h(t)
T
2T
1.5T
k(t)
t
T
E
0.5E
0

Exercices
Asservissement & Régulation Page: 58 Propose par: SOYED-Abdessamï
Exercice 4:
Soit un processus industriel modélisé par l'équation différentielle suivante: dy
2 +y=5u
dt
1. Etablir la fonction de transfert de ce processus.
2. Donner la réponse de ce processus (conditions initiales nulles) pour une entrée de la forme:
Exercice 5:
On considère un système industriel modélisé par l'équation différentielle suivante:
2
2
d y dy du
+6 +9y=8 +8u
dt dt dt
.
1. Etablir la transformée de Laplace de l’équation précédente,
2. En déduire l'expression de la sortie pour entrée (impulsion de Dirac unitaire), on suppose
que toutes les conditions initiales sont nulles),
3. Retrouver les valeurs initiale et finale de y(t), en appliquant les théorèmes de la valeur
initiale et finale,
4. Etablir et tracer l’allure de y(t), en déduire sa valeur minimale.
0
E=10
T=0.1
t
u(t)

Exercices
Asservissement & Régulation Page: 59 Propose par: SOYED-Abdessamï
Exercice 6:
Soit un système automatisé est modélisé par l’équation différentielle: 2
2
d x dx
M +h +kx=f(t)
dt dt
, il
est donnée par la figure ci-dessous:
1. Déterminer la fonction de transfert:
X(p)
H(p)=
F(p)
, en fonction des paramètres du système,
2. Mettre la fonction de transfert sous la forme canonique: 2
0
2 2
0 0
K.w
H(p)=
p +2mw .p+w
.
Avec K: gain statique, m: facteur d’amortissement et w0: pulsation propre,
3. En déduire les expressions de (K, m et w0 ) en fonction des paramètres (k, h et M),
4. Etablir l’expression de 2
0
2 2
0
K.w
H(p)=
(p+a) +w
, pour K=1, m=0.5 et 2
0
w =1(rad/s)
et identifier les
valeurs de a et w0.
5. Etablir l’expression de x(t), pour une entréef(t)=
δ(t)
, donner son régime de fonctionnement
et calculer la valeur de x(+), conclure sur la stabilité de système,
Polie
k
Solide de
Masse: M
Liquide
M

Exercices
Asservissement & Régulation Page: 60 Propose par: SOYED-Abdessamï
Le schéma fonctionnel du système en boule fermée est donné par la figure ci dessous:
6. Etablir la transmittance du système en boule fermée: 2
B B
2 2
B B B
k w
T(p)=
p +2m w .p+w
,
7. En déduire les paramètres kB, mB et wB en fonction de (K, m et w0).
8. Etablir l’expression de x(t) en boucle fermée pour un échelon
f(t)=10.u(t)
, en déduire son
allure.
Exercice 7:
Soit un système asservi donné par le schéma fonctionnel suivant:
1. Déterminer l’expression T(p) en boucle fermé,
2. Etablir l’équation caractéristique du système,
3. Etudier la stabilité, en utilisant le critère de Routh,
4. Donner la condition sur  pour que le système soit stable.
H(p)
F(p) X(p)
E(p) S(p)
1λ.pp
1
2
1p1