devoir controle n°2(2019-2020)

1/4
Le sujet comporte 4 pages numérotées de 1/4 à 4/4.
La page 4/4 à remplir par le candidat et à remettre avec sa copie
CHIMIE : (9 points)
Exercice n°1 :(5,5 points)
1) a- Pour les couples acide-base suivants, compléter (sur votre copie), l’espèce chimique
manquante :
 couple 1 : C6H5COOH/………………… pKa1=4,2
 couple 2 : ……………/CH3COO- pKa2=4,8
 couple 3 : NH
/………….. pKa3=9,25
b- Classer ces couples par ordre croissant de force de la forme acide.
2) a- Ecrire l’équation bilan de la réaction qui se produit entre la forme acide du couple 2
et la base du couple 3.
b- Exprimer sa constante d’équilibre K en fonction de pKa2 et pKa3. Calculer sa valeur
puis conclure.
3) Par dilution successives d’une solution(S) d’un monoacide de formule chimique notée AH, on
prépare différentes solutions. Pour chacune de ces solutions, supposées faiblement diluées, on
mesure le pH et on détermine le taux
d’avancement final τf correspondant.
Les résultats obtenus ont permis de tracer
la courbe de la figure 1 traduisant l’évolution
de log τf en fonction de log C.
(C désigne la valeur que peut prendre la
concentration de chacune des solutions préparées)
a- Dresser le tableau descriptif d’avancement
volumique noté y. relatif à la réaction de monoacide
AH avec l’eau.
b- Montrer que la constante d’acidité du couple
AH/A- est : Ka= C.τ
f
τf ;
c- En précisant l’approximation utilisée, déduire que log τf= 
log (Ka
C).
d- Justifier l’allure de la courbe de la figure1.
e- Déterminer la valeur du pKa du couple AH/A-. En déduire la formule chimique de l’acide AH.
Exercice n°2 :(3,5 points)
Toutes les solutions sont prises à 25°C, température à laquelle le produit ionique de l'eau pure
est Ke =10-14.
On considère deux solutions aqueuses (S1) et (S2) de même pH = 2,9 :
- (S1) est une solution aqueuse d’un monoacide A1H ;
- (S2) est une solution aqueuse d’un monoacide A2H.
On prélève séparément un volume V0=10mL de chacune de ces solutions et on complète dans
chaque cas avec de l’eau distillée jusqu'à avoir un volume V=200mL de solution. On obtient ainsi
deux nouvelles solutions (S'
) et (S' ) de pH' =4,2 et pH' = 3,6.
Direction régionale de Béja
Epreuve : Sciences physiques
Niveau: 4ème Sc.exp1+2
DEVOIR DE CONTROLE N° 2
Durée:2 heuresCoefficient: 4 Date : 30 /01/2020
PROF : TRAYIA NABIL
Lycée secondaire
Ammar Farhat Nefza
-1,65
-2
-1, 5
-1
logτf
log C
-1,4
Figure 1
-1,3

2/4
On suppose que l’on pourra négliger les ions dus à l’ionisation propre de l’eau.
1)- a- Calculer la quantité de matière n0 d’ions hydronium H3O+ contenus dans le prélèvement
de volume V0 de (S1) et de (S2).
b- Calculer les quantités de matières n1 et n2 d’ions H3O+ contenus respectivement dans
les solutions (S'
) et (S' ).
c- En déduire que A1H est un monoacide fort tandis que A2H est un monoacide faible.
d- Calculer la concentration C1 de la solution aqueuse (S1) du monoacide A1H.
2)- Sachant que le monoacide A2H est l’acide éthanoïque CH3COOH et la concentration de (S2)
est C2 = 0,1mol.L-1.
a- Ecrire l’équation de la réaction de l’acide éthanoïque avec l’eau.
b- Calculer τf et vérifier que l’acide éthanoïque est faiblement ionisé dans l’eau.
3)- Calculer le taux d’avancement final τ'
f de la réaction de l’acide éthanoïque avec l’eau dans la
solution (S'
) et déduire l’effet de la dilution sur l’ionisation de l’acide éthanoïque dans l’eau.
PHYSIQUE : (11points)
Exercice n°1 :(7 points)
Dans une séance de travaux pratiques, on se propose d’étudier les oscillations électriques forcées en
régime sinusoïdal d’un circuit RLC série. Ce circuit comporte :
- un résistor de résistance R=37,5,
- une bobine d’inductance L et de résistance r,
- un condensateur de capacité C,
- un générateur de basses fréquences (GBF)
délivrant une tension sinusoïdal u(t) = U  sin(2Nt + φu)
de fréquence N réglable et de valeur efficace U constante.
A l’aide d’un oscilloscope bicourbe, convenablement branché, on visualise
simultanément les variations en fonction du temps des tensions u(t) aux bornes du générateur et
uD(t) aux bornes du dipôle D constitué par l’ensemble {résistor + bobine} sur la voie (Y).
1)- Reproduire la figure 1 et indiquer les connexions effectuées à l’oscilloscope
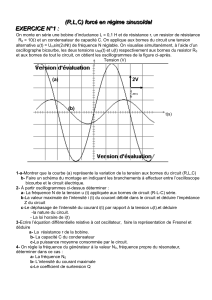
2)- Pour une fréquence N=N1=198Hz de la fréquence du générateur, on obtient les courbes (c1)
et (c2) de la figure 3 représentent les variations, au cours du temps, des deux tensions uD(t) et u(t).
Dans ce cas le voltmètre indique une tension UR=4,5V.
a- Montrer que la courbe (c2) correspond à u(t).
b- Déterminer :
 Les valeurs maximales de u(t) et uD(t).
 Le déphasage Δφ=φD - φu de la tension
uD(t) par rapport à la tension u(t).
c- Donner les expressions en fonction de temps
de u(t) et uD(t).
d- Déduire la valeur de l’intensité efficace I du courant
qui traverse le circuit.
3)- En appliquant la loi des mailles, établir l’équation
différentielle relative à l’intensité de courant i(t)
qui circule dans le circuit.
4)-
a- Sur la feuille annexe, représenter la construction de Fresnel relative aux tensions maximales en
respectant l’échelle 1cm V .On désignera par :
OA le vecteur associé à u (t).
OC le vecteur associé à uD(t).
CA le vecteur associé à uC(t) tension aux bornes du condensateur.
BC le vecteur associé à uL(t) tension aux bornes de la bobine.
(L, r)
C
R
GBF
V
i
῀
Figure 1
0
72
10 2
Tension (en V)
Temps
(c1)
(c2)
Figure 3

3/4
b- En exploitant la construction de Fresnel, montrer que :
 la valeur de la capacité C du condensateur est C= 8μF.
 la valeur de l’inductance de la bobine est L=27mH et déduire sa résistance interne r.
5)- En faisant varier la fréquence N, on constate que le voltmètre indique une tension UR=7,75V
pour une fréquence N2.
a- Déterminer l’impédance Z du circuit et déduire que le circuit est en état de résonance
d’intensité.
b- Déterminer la fréquence N2.
Exercice n°2 :(4 points)
Une portion de circuit est formée d’une bobine d’inductance L et de résistance r=10Ω, d’un
condensateur de capacité C et d’un résistor de résistance R, montés en série. Un générateur basses
fréquences (GBF) impose aux bornes de cette portion de circuit une tension alternative u(t) de
fréquence N réglable et d’amplitude Um=12V.
A l’aide d’un dispositif approprié, on suit en fonction de N, l’évolution de :
L’intensité maximale Im du courant traversant le circuit ;
La charge maximale Qm emmagasinée dans le condensateur.
Les courbes obtenues sont représentées sur la figure 4.
1)- Justifier que la courbe C1 correspond à Im=f(N).
2)- En exploitant les courbes de la figure 4, déterminer les valeurs de R, L et C.
3)- On prendra dans ce qui suit : R=390Ω, L=0,6H et C=0,58μF.
Pour une valeur N1 de N, la tension u(t) est en avance de phase de π
 rad par rapport à la tension
uC(t) aux bornes du condensateur.
a- Préciser, en le justifiant, la nature du circuit (résistif, capacitif ou inductif).
b- Déterminer l’impédance Z du circuit et déduire la valeur de N1.
c- déterminer la valeur maximale UCm de la tension uC(t).
350
30
Im(10-3A)et Qm(10-6C)
150
200
25
20
15
10
5
250
300
N (Hz)
(c1)
(c2)
Figure 4

4/4
Feuille annexe (à rendre avec la copie)
Nom et Prénom : ……………………..……………………………….classe : ……………..
φu
Echelle : 1cm
V