widad 1

IUT de Nancy-Brabois Fabrice Sincère http://perso.orange.fr/fabrice.sincere/ page 1/8
E XERCICES D ’E LECTRICITE
R EGIME CONTINU
E NONCES
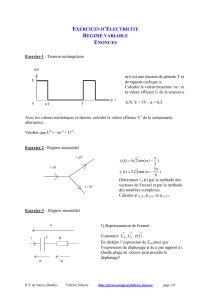
Exercice 1 : Déterminer la résistance équivalente du dipôle AB :
Exercice 2 : Calculer I
1
, I
2
et I
3
:
Application numérique :
E = 6 V, R
1
= 270 Ω,
R
2
= 470 Ω et R
3
= 220 Ω.
Exercice 3 : Une boîte noire contient trois dipôles E, R
1
et R
2
.
E = 6 V ; R
1
et R
2
sont inconnues.
Avec le voltmètre on mesure 4,00 V.
Avec l’ampèremètre on mesure 0,50 A.
En déduire R
1
et R
2
.
A B
3,9 kΩ
1 kΩ
1,5 kΩ
3,3 kΩ
R
1
R
2
R
3
I
1
I
2
I
3
E
R
1
R
2
E
A
B
VA

IUT de Nancy-Brabois Fabrice Sincère http://perso.orange.fr/fabrice.sincere/ page 2/8
Exercice 4 : Déterminer la puissance P consommée par R
C
(en fonction de E, R
C
et R) :
Pour quelle valeur de R
C
la
puissance consommée est-elle
maximale ?
Que vaut alors P
max
?
Exercice 5 : Chercher les modèles de Thévenin et de Norton des circuits suivants :
Les batteries d’accumulateurs
sont identiques (f.e.m. 12 V
et résistance interne 15 mΩ).
Exercice 6 : Déterminer les modèles de Thévenin et de Norton du circuit suivant :
A.N. E = 12 V, I
1
= 3 mA, R
A
= 1,5 kΩ, R
B
= 1 kΩ et R
C
= 3 kΩ.
R=100Ω
R
C
: résistance
réglable
R
A
E=10 V
R
B
E
I
1
R
C
A
B
A
B
A
B

IUT de Nancy-Brabois Fabrice Sincère http://perso.orange.fr/fabrice.sincere/ page 3/8
Exercice 7
Calculer l’intensité du courant dans la branche AB en appliquant :
• les lois de Kirchhoff
• le théorème de Millman
• le théorème de superposition
Exercice 8 : Pont de Wheatstone
Déterminer le modèle de Thévenin du dipôle AB.
A quelle condition sur R a-t-on U
AB
= 0 V ?
A.N :
U
AB
s’annule pour R = 8,75 kΩ.
En déduire X la valeur de la résistance inconnue.
A
B
X
P=1 kΩ
R
Q=10 kΩ
E
4 V
B
A
16 Ω4 Ω
6 Ω24 V

IUT de Nancy-Brabois Fabrice Sincère http://perso.orange.fr/fabrice.sincere/ page 4/8
C ORRIGES
Exercice 1
Entre A et B, nous avons les résistances 3,9 kΩ et 1 kΩ en parallèle, en série avec
les résistances 1,5 kΩ et 3,3 kΩ en parallèle.
R
AB
= (3 ,9 kΩ // 1 kΩ) + (1,5 kΩ // 3,3 kΩ) = 1,827 kΩ
Exercice 2
Notons R la résistance équivalente à l’association en parallèle de R
2
et R
3
: R = R
2
//R
3
≈150
Ω.
Appliquons la loi d’Ohm : E = (R
1
+R) I
1
A.N. I
1
= 14,29 mA
Appliquons maintenant la formule du diviseur de courant :
1
32
3
1
32
2
2I
RR R
I
GG G
I+ =
+
=
A.N. I
2
= 4,56 mA
Loi des nœuds : I
3
= I
1
- I
2
= 9,73 mA
Exercice 3
Un ampèremètre (parfait) se comporte comme un court-circuit (résistance interne nulle):
Loi d’Ohm : E = R
1
I
A.N. R
1
= 12 Ω.
Un voltmètre (parfait) ne consomme pas de courant (résistance interne infinie):
On reconnaît un diviseur de tension : E
RR R
U
21
2
+
=
R
1
R
E
I
1
R
1
R
2
E
U=0 V
I=0,5 A
A
R
1
R
2
E
U=4,00 V
V
I=0

IUT de Nancy-Brabois Fabrice Sincère http://perso.orange.fr/fabrice.sincere/ page 5/8
D’où :
12
R
U
E
U
R− =
A.N. R
2
= 24 Ω.
Exercice 4
P = UI
Formule du diviseur de tension : E
RR R
U
C
C
+
=
Loi d’Ohm : E = (R+R
C
) I
D’où : P = ²E
)²RR( R
C
C
+
Notons P’(R
C
) la dérivée de P par rapport à R
C
.
P est maximum quand la dérivée est nulle.
²E
)RR( ²R2)²RR(
)R('P
4
C
CC
C
+
−
+
=
P’(R
C
) = 0 ⇒ R
C
= R = 100 Ω
W 25,0
R
4
²E
P
max
==
Exercice 5
R
R
C
E
I
U
2E=24 V
2r =30 m Ω
E
r
E
r
=
E, r
E, r
=
30
m Ω
I
cc
=800 A
=
MET MEN
800 A 1600 A
15
m Ω
7,5 m Ω
=
E, rE, r
=
800 A
15
m Ω
E=12 V
r/2=7,5 m Ω
=
MEN MET