Transformations cours à trous

Transformations
En mathématiques, une transformation est un processus qui a tout point donné
M associe un unique point M’. On a étudié en cinquième deux
transformations : la symétrie axiale et la symétrie centrale.
En troisième, nous étudierons trois nouvelles transformations :
• l’homothétie.
• la translation.
• la rotation.
I)Homothétie :
a) Définition :
Définition :
……………………………………………………………………………………………………………
…………………………………………………………………………………………………………….
…………………………………………………………………………………………………………….
…………………………………………………………………………………………………………….
…………………………………………………………………………………………………………….
…………………………………………………………………………………………………………….
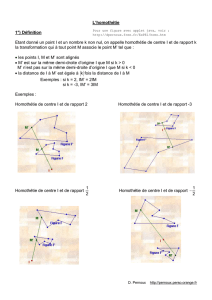
Exemple n°1 :
Cas d’une homothétie h de centre O et de rapport k = 3, notée h(O ;3) :
* Les points O, A et A’ sont alignés.
* k = 3 > 0 donc O ∉ [AA’].
* OA’ = 3OA.
* On écrit A’ = h(A).

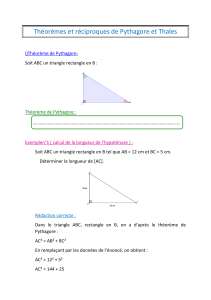
Exemple n°2 :
Cas d’une homothétie h de centre O et de rapport k = –2, notée h(O ;–2) :
* Les points O, A et A’ sont alignés.
* k = –2 < 0 donc O ∈ [AA’].
* OA’ = 2OA.
* On écrit A’ = h(A).
b) Image d’une figure par une homothétie :
Propriété :
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
……………………………………………………………………………………………………………….
Exemple n°1 :
Cas d’une homothétie de centre O et de rapport k = 2 :
Le triangle A’B’C’ est l’image du
triangle ABC par l’homothétie
de centre O et de rapport k = 2.
Le triangle A’B’C’ est un
agrandissement du triangle ABC
de rapport 2 ( les dimensions
du triangle ABC ont toutes été
multipliées par 2 ).

Exemple n°2 :
Cas d’une homothétie de centre O et de rapport k = –0,5 :
Le triangle A’B’C’ est l’image du triangle
ABC par l’homothétie de centre O et de
rapport k = – 0,5.
Le triangle A’B’C’ est une réduction du
triangle ABC de rapport 0,5 ( les dimensions
du triangle ABC ont toutes été multipliées
par 0,5).
c) Propriétés des homothéties :
Propriété :
……..…………………………………………………………………………………………………………….
………..………………………………………………………………………………………………………….
……………..…………………………………………………………………………………………………….
………………..………………………………………………………………………………………………….
……………..…………………………………………………………………………………………………….
………………..………………………………………………………………………………………………….
Exemple :
La droite (A’B’) est l’image de la droite
(AB) par l’homothétie h(O ; k ).
Les droites (AB) et (A’B’) sont
parallèles.
On constate également que
l’homothétie conserve l’alignement des
points car l’image d’une droite est une
droite.

II)Translation:
a) Définition :
Définition :
……………..…………………………………………………………………………………………………….
………………..………………………………………………………………………………………………….
……………..…………………………………………………………………………………………………….
Exemple :
M a pour image M’ par la translation qui transforme A en B.
Autrement dit, dans la translation qui transforme A en B, un point M a pour
image M’ tel que :
• on se déplace de A vers B dans la même direction et le même sens
que de M vers M’.
• les distances AB et MM’ sont égales.
b) Propriété :
Soit CDE un triangle et A, B deux
points donnés.
C’D’E’ est l’image de CDE par la
translation qui transforme A en
B.

On constate que les deux triangles sont identiques.
Propriété :
……………..…………………………………………………………………………………………………….
………………..………………………………………………………………………………………………….
……………..…………………………………………………………………………………………………….
………………..………………………………………………………………………………………………….
……………..…………………………………………………………………………………………………….
………………..………………………………………………………………………………………………….
……………..…………………………………………………………………………………………………….
………………..………………………………………………………………………………………………….
III) Rotation:
a) Définition :
Définition :
……………..…………………………………………………………………………………………………….
………………..………………………………………………………………………………………………….
……………..…………………………………………………………………………………………………….
………………..………………………………………………………………………………………………….
……………..…………………………………………………………………………………………………….
………………..………………………………………………………………………………………………….