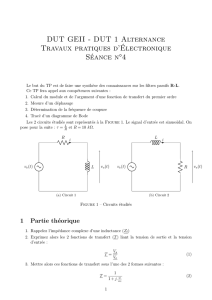
Analyse Fréquentielle des Circuits Électriques - Diagramme de Bode
Telechargé par
louis.bessiene

Définitions
Le diagramme de Bode.
Préambule
Le décibel
Fonctions de transfert.
Principe
Principe
En électronique, on étudie le comportement dynamique
d’un système, en effectuant le rapport entre une grandeur
d’entrée et une grandeur de sortie en fonction de la
fréquence de fonctionnement du système.
On arrive facilement à modéliser ce rapport par une
fonction fractionnaire complexe. Afin de mieux
appréhender la modélisation obtenue, celle-ci est
représentée de diverses façons (module en fonction de la
fréquence, argument en fonction de la fréquence ...).
C’est l’objet de ce cours : maitriser une des
représentations graphiques les plus courantes.
Mickaël Grisel Analyse fréquentielle page : 5/27 - Diapo : 4/17
 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
 13
13
 14
14
 15
15
 16
16
 17
17
 18
18
 19
19
 20
20
 21
21
 22
22
 23
23
 24
24
 25
25
 26
26
 27
27
1
/
27
100%