COURS ET TD TORSION

L
A
T
ORSION
S
IMPLE
C
OURS
G
ENIE
M
ECANIQUE
(1213) Page1/8 F
LEXIO N
P
LANE
S
IMPLE
LaboratoireMécaniquedeKORBA http://mimfs.jimdo.com/ Proposépar M
r
BenAbdallahMarouan
IMISEENSITUATION:
Ondonneledessind’ensemblepartielcidessousàl’échelle1:3delaboitedesvitessesd’untour(L180).
NB:
Ennégligeantlesforcesnormalesàl’axe,l’arbre(1)estmodélisécommesuit
:
Fig.1
S0
MA
Lignemoyenne S
MB
II.1Déduireletypedelasollicitationàlaquelleestsoumisl’arbre(1):..................................;
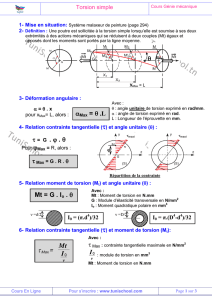
IIDEFORMATIONANGULAIREDUEALATORSION:
II.1
 Expérience
:
Placeruneéprouvetteàtraverslesélémentsdefixationetlabloquéedanslaportéfixe.
Fixerl’autreboutauleviermontédansdesroulementsàbilles(àla
longueurdésirée).
Réglerledispositifdemesuredetellesortequelepalpeurdu
comparateurestexactementenfacedel’entailledulevier.
Baisserlecomparateuretréglerl’aiguilleàzéro.
Remar que:
1tourdel’aiguilledecomparateurcorrespondà1°.
Pourunechargedonnée(
10N
);Compléterletableaucidessous:
l
(enmm)
a
(endegr é)
600 ..........
500 ..........
400 ..........
II.2Constatation:
Sousl’actiondelatorsion,lesfibresd’uncylindre,parallèleàsonaxegéométrique,s’enroulentsuivantdeshélicesautourdecet
axe.Seulelafibreaxialerestedroite
:
c’estlafibreneutre
.
5
30
21
35
8
41 2 3 6 34
10
9
23
64 7
32

L
A
T
ORSION
S
IMPLE
4
E
S
CIENCES
T
ECHNIQUES
C
OURS
G
ENIE
M
ECANIQUE
(1213) Page2/8 F
LEXIO N
P
LANE
S
IMPLE
LaboratoireMécaniquedeKORBA http://mimfs.jimdo.com/ ProposéparM
r
BenAbdallahMarouan
Z
Y
Répartitiondescontraintes
G
tMaxi
M
tMaxi
r
II.3Etudedescontraintes:
Considér onsletr onçon(2)delapoutr er epr ésentéecicontre;
l’équilibr edesetr onçonimpliqueq ueleseffor tsdecohésions
déduisentunmomentM
tx
.
AupointM,l’effor télémen tair edf,r elatifàl’élémen tdesur facedSest
dansleplandelasection(S)etper pendiculair eaur ayonGM=ρ:(r ho).
Ler appor t:
(Taux)estlacontr aintetangentielaupointM.
II.4Relationcontr aintedéfor mation:
Ondémontr equelacontr aintedetor sionenunpointMd’unesectionestper pendiculair e
àladistanceρdupointmàl’axedecylindr eetdel’angleunitair edetor sionθ.
Gétantlemoduled’élasticitétr ansversal.
Lacontr ainte
t
estmaximalepourρ=r .
Diagr a mmeder épar titiondescontr aintes
dansunesectiondr oite.
L’épr ouvetteestuncylindr ed’axexx’,desectionconstanteS.
SoientS
0
etSdeuxsectionsdr oitesdistantesde
l
et[m
0
m]une
génér atr ice.Sous
l’actiondescouples(F,F’)(F
1
,F’
1
)desenscontr air esSatour né
d’unangle
a
par r appor tàS
0
pr isecommer éfér ence.
L’expér iencemontr equepour unmomentetunesectiondonnés
:
=
l
a
=
1
1
l
a
=
q
en[rd/mm]:Angleunitairedetorsion
a
en(r d)(angleder otationentr edeuxsections)
df
M
z
(2)
G0
G0
x
y
Mt
G1
(1)
SectiondroiteS
1/2
x
1/2
M
z
df
ds
r
G
y
q t Grmax =(3)
rq t G =(2)
x'x
F'
1
O0
F'
O
a
O1
S1
F
S0
m0
1
l
a1
d
m m1
S
l1
F
Fig1
τ
dS
df
= (1)

L
A
T
ORSION
S
IMPLE
4
E
S
CIENCES
T
ECHNIQUES
C
OURS
G
ENIE
M
ECANIQUE
(1213) Page3/8 F
LEXIO N
P
LANE
S
IMPLE
LaboratoireMécaniquedeKORBA http://mimfs.jimdo.com/ ProposéparM
r
BenAbdallahMarouan
II.5Relationcontrainte–momentdetorsion:
(
I
0
/v
)estlemoduledetor sion delasectionconsidér éeen(m m
3
)
Dansl’hypothèsed’unedéfor mationélastique,lemomentducoupledetor sionestdonnépar lar elation:
Enutilisantlesr elations(2)et(4)l’expr essiondelacontr aintede
glissementenunpointd’unesectiondr oitesituéeàunedistance
r
dela
fibr eneutr eapour expr ession:
Cettecontr ainteestmaximalepour unpointdelafibr elapluséloignéedelafibr eneutr e;soitendésignant
r
Maipar
v
sadistanceàcetaxe:
II.6La conditionder ésistanceàlator sion:
Pour qu’uncylindr er ésisteentoutesécur itéàuncoupledetor siondonné,ilfautquelar elationsuivantesoitvér ifiée:
t
max
£
R
pg
avec
R
pg
:larésistancepr atiqueauglissementen(N/mm²)
Avec Rpg= s
gRe
Rpg:r ésistancepr atiqueauglissement........en[MPa]
Reg:lim iteappar ented’élasticitéauglissementen[MPa ]
s
:coefficientdesécur ité................[sansunité]
II.7Momentquadratiquepolaire:
Ä
V
ALEUR
D
U
M
OMENT
Q
UADRATIQUE
P
OLAIRE
D
E
S
URFACES
É
LEMENTAIRES
S
URFACES
I
O
V
v
Io
32
. 4 d p
2
d
16
. 3 d p
32
).( 44
dD
- p
2
D
D
dD
.16
).( 44 - p
Aretenir:
q
=
L
a
t
Maxi
=G.
q
.r Mt=G.
q
.Io
t
Maxi
=
v
Io
Mt
avecv=r Conditionder ésistance
t
Maxi
£
Rpg
Conditionder igidité
q £ q
lim
avec
q
=
IoG
Mt
.
Avec:
M
t
:
lemomentd ucoupledetor sionen(N.mm).
G
:lemoduled’élasticitétr ansversaleen(N/mm²).
I
0
:lemomen tquadr atiquepolair ed’unesectiondr oiteen(mm
4
).
Mt=GθIo
(4)
v
MtMt
vτmax I
I 0
0
= =
Avec:Mten(N.mm),I
0
en(mm
4
)et
r
en(mm)
(5)
I
Mt
0
r t =

L
A
T
ORSION
S
IMPLE
4
E
S
CIENCES
T
ECHNIQUES
C
OURS
G
ENIE
M
ECANIQUE
(1213) Page4/8 F
LEXIO N
P
LANE
S
IMPLE
LaboratoireMécaniquedeKORBA http://mimfs.jimdo.com/ ProposéparM
r
BenAbdallahMarouan
IIIA
PPLICATION
:
III.1Agitateur pour peintur e
Unetiged’agitateurpourpeintureestmontéeenboutdemandrinsuruneperceusedebricolage.Lalongueurdelatigeestde
700mm
.Lapuissancetransmiseestde
500watts
à
1500tr /mn
.Larésistancepratiqueauglissementdumatériaudelatigeestde
R
pg
=5daN/mm².
1
Déterminerlediamètreminimaldelatige.
d
min
:
..........................................................................................................
..........................................................................................................
..........................................................................................................
..........................................................................................................
..........................................................................................................
2
Calculerl’
angledetor sion
entrelesdeuxextrémitésdelatige(
G=8000daN/mm²
):
a
..........................................................................................................
..........................................................................................................
..........................................................................................................
..........................................................................................................
3
Calculerle
diamètr edelatige
danslecasoul’angleunitairedetorsion nedoitpasdépasserlavaleurde
0,1degr é
par
mètr e
.
..........................................................................................................
..........................................................................................................
..........................................................................................................
..........................................................................................................
..........................................................................................................
700

L
A
T
ORSION
S
IMPLE
4
E
S
CIENCES
T
ECHNIQUES
C
OURS
G
ENIE
M
ECANIQUE
(1213) Page5/8 F
LEXIO N
P
LANE
S
IMPLE
LaboratoireMécaniquedeKORBA http://mimfs.jimdo.com/ ProposéparM
r
BenAbdallahMarouan
III.2Ar br eInter médiair e:
Un
ar brepleindedia mètr ed
etdelongueur
L
égaleà
2m
transmetune
puissance
de
20kw
àla
vitesse
de
1500tr /mn
entreun
récepteuretunmoteur.L’arbrereposesurdeux
paliersA
et
B
.
Larésistancepratiqueauglissementdumatériaudel’arbreestde
R
pg
=8daN/mm²
.
1
Calculerlecoupledetorsionagissant surl’arbre(
Mt
)
..........................................................................................................
..........................................................................................................
..........................................................................................................
..........................................................................................................
2
Déterminerle
diamètr emini
del’arbreetcalculerl’
angledetorsion
entreAetBsachantque
G=8000da N/mm².
..........................................................................................................
..........................................................................................................
..........................................................................................................
..........................................................................................................
..........................................................................................................
3
Sil’onimposeà
l’angledetor sion
lavaleurmaximalede
0,1degr épar mètr e
,déterminerlediamètre
d
danscecas.
..........................................................................................................
..........................................................................................................
..........................................................................................................
..........................................................................................................
..........................................................................................................
..........................................................................................................
Recepteur
L=2000
Moteur A
d
B