EXERCICEN

EXERCICEN°1 : (7,5 pts)
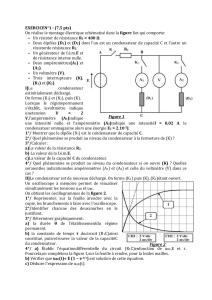
On réalise le montage électrique schématisé dans la figure 1et qui comporte:
− Un résistor de résistance R1 = 400 Ω.
− Deux dipôles (D1) et (D2) dont l'un est un condensateur de capacité C et l'autre un
résistorde résistance R2.
− Un générateur de f.é.m.E et
de résistance interne nulle.
− Deux ampèremètres(A1) et
(A2).
− Un voltmètre (V).
− Trois interrupteurs (K),
(K1) et (K2).
I]Le condensateur
estinitialement déchargé.
On ferme (K1) et (K2), puis (K).
Lorsque le régimepermanent
s'établit, levoltmètre indique
unetension U = 2
V,l'ampèremètre (A1)indique
une intensité nulle et l'ampèremètre (A2)indique une intensitéI = 0,02 A. le
condensateur emmagasine alors une énergie EC = 2.10-5J.
1°/ Montrer que le dipôle (D1) est le condensateur de capacité C.
2°/ Quel phénomène se produit au niveau du condensateur à la fermeture de (K) ?
3°/Calculer :
a)La valeur de la résistance R2.
b) La valeur de la f.é.m.E.
c)La valeur de la capacité C du condensateur.
4°/ Quel phénomène se produit au niveau du condensateur si on ouvre (K) ? Quelles
seraientles indicationsdes ampèremètres (A1) et (A2) et celle du voltmètre (V) dans ce
cas ?
II]Le condensateur est de nouveau déchargé. On ferme (K1) puis (K), (K2)étant ouvert.
Un oscilloscope à mémoire permet de visualiser
simultanément les tensions uAB et uBC.
On obtient les oscillogrammes de la figure 2.
1°/ Représenter, sur la feuille àrendre avec la
copie, les branchements à faire avec l'oscilloscope.
2°/Identifier chacune des deuxcourbes en le
justifiant.
3°/ Déterminer graphiquement:
a) la durée θ de l'établissementdu régime
permanent.
b) la constante de temps τ ducircuit (R1C)ainsi
constitué, puisretrouver la valeur de la capacitéC
du condensateur.
4°/ a) Établir l'équationdifférentielle du circuit (R1C)enfonction de uBC,E et τ.
Pourcela,on complétera la figure 1,sur la feuille à rendre, pour la loides mailles.
b) Vérifier que uBC(t)= E (1 ‒ e-t/τ) est solution de cette équation.
c) Déduire l'expression de uAB(t).
Figure 1
Figure 2

EXERCICEN°2 : (5,5 pts)
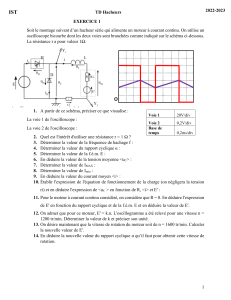
Dans le but de déterminer l'inductance L etla
résistance r d'une bobine, on réalise
deuxexpériences avec le circuit de la figure 3.
Un oscilloscope bicourbe permet devisualiser
les tensions u1 et u2.
Expérience A : G est un générateur detension
continue et R = 100 Ω.
1°/ Donner les expressions de u1(t) et u2(t)en
fonction de i(t).
2°/ Montrer que la résistance r de la bobinea
pour expression:
3°/Lorsque le régime permanent s'établiton
trouve u1= 1 V et u2= ‒ 5V.
a) Que devient l'expression (1) en régimepermanent?
b) Déduire la valeur de r.
c) Quel est le phénomène responsable du retard de l'établissement du
régimepermanent?
Dans quel dipôle se manifeste-t-il ?
Pour la suite de l'exercice, on prendra r = 20 Ω.
Expérience B : G est un générateur
bassesfréquences (G.B.F) délivrant une
tensiontriangulaire. On modifie la valeur de R
demanière à avoir R = r.
On observe alors l'oscillogramme de la figure 4 sur
laquelle seule u2 estreprésentée.
1°/ Déterminer la fréquence de la tensiondélivrée
par le G.B.F.
2°/L’oscillogramme suivant, figure 5,
permetd'obtenir la tension sommeuS = u1 + u2.
a) Montrer que:  
 .
b) En exploitant les figures 4 et 5 et larelation
précédente, déterminer la valeurde L.
c) Calculer l'énergie Elemmagasinéepar la bobine
lorsque la tension u2 atteintsa valeur maximale.
Figure 3
Figure 4
Figure 5