Chapiter d'introduction : Mesures et incertitudes

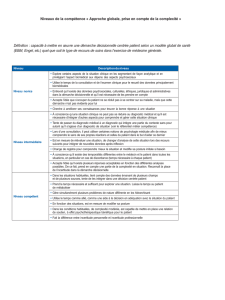
Chapitre d’introduction
Page 1 sur 4
Chapitre d’introduction. Mesures et incertitudes
En physique et en chimie, toute grandeur, mesurée ou calculée, est entachée d’erreur, ce qui ne l’empêche
pas d’être exploitée pour prendre des décisions. Le but de ce chapitre est de définir la notion d’erreur et
d’apprendre à estimer ou à calculer l’incertitude de mesure associée.
I. Définitions
1. Intervalle de confiance et incertitude absolue
Qu’elles soient mesurées ou calculées, les valeurs des grandeurs ne sont connues qu’avec une précision
limitée.
En effet, du fait des fluctuations de tout phénomène et des imperfections de mesures, l’expérimentateur
n’a accès qu’à des valeurs estimées de grandeurs dont il peut donner un encadrement avec un bon niveau
de confiance.
Cet encadrement s’appelle l’intervalle de confiance dans lequel il estime que la valeur vraie de la grandeur
se trouve. Le résultat de la mesure se donne alors sous la forme suivante :
L’incertitude absolue sur la grandeur  se note . Elle peut également se noter , la lettre «  » étant
la première lettre du mot « uncertainty » en anglais (qui signifie incertitude).
Exemple : Résultat d’une mesure à l’aide d’un voltmètre :   . Cela signifie que la tension
 est comprise entre ............... et ................. .
Remarque : Lorsque la valeur d’une grandeur est fournie sans incertitude, cette dernière est, par
convention, égale à une demi-unité du dernier chiffre significatif exprimé. Exemple :    signifie
  .
2. L’incertitude relative
L’incertitude relative,  
, caractérise la précision d’une mesure. Plus elle est petite, plus la mesure est
précise.
Elle n’a pas d’unité et s’exprime souvent en pourcentage.
Si  
  soit 1%, alors la mesure est de bonne qualité.
Application : Déterminer l’incertitude relative sur la valeur de la tension    .

Chapitre d’introduction
Page 2 sur 4
II. Estimation de l’incertitude
Suivant que la mesure est faite une seule fois ou répétée un grand nombre de fois, l’incertitude ne s’évalue
pas de la même manière.
1. Mesures effectuées une seule fois
L’incertitude d’une mesure unique conjugue deux sources d’informations :
- des informations techniques sur l’instrument de mesure données par le fabricant ou connues
conventionnellement ;
- des informations subjectives sur l’appréciation de la façon dont la mesure a été effectuée.
Exemple : L’incertitude de lecture sur un instrument analogique (règle graduée, aiguille sur un cadran...)
est, par convention, au minimum une demi-unité de graduation. Pour les instruments numériques, la
notice de l’appareil indique comment calculer l’incertitude.
Application :
- Mesurer la largeur L d’une feuille de papier à l’aide d’une règle graduée au millimètre près. Estimer
l’incertitude et écrire le résultat de la mesure.
- Exprimer le résultat pour la valeur  lue sur un multimètre dont la notice indique : « Précision,
toutes gammes : ± 0,5 % de la valeur affichée + 1 digit » ?
Aide : L’indication 0,5 % traduit une incertitude relative de 0,005, et le digit à ajouter correspond au
dernier chiffre exprimé de la mesure, soit .
2. Mesures effectuées plusieurs fois
Une mesure peut être répétée à quelques reprises ou un grand nombre de fois. La répétition des mesures
améliore la précision de la mesure, ce qui est indispensable pour un dispositif de mesure peu fidèle.
La moyenne des valeurs mesurée est la meilleure estimation qui puisse être faite.
L’incertitude se calcule selon une règle dépendant de la situation (au baccalauréat, elle sera donnée
chaque fois).
III. Calculs d’incertitudes
1. Incertitudes dans les calculs
Pour une grandeur obtenue par calcul, l’incertitude sur la valeur de cette grandeur se calcule grâce à une
relation mathématique (au niveau du baccalauréat, la relation qui permet de calculer l’incertitude est
fournie, seule son application doit être sue).

Chapitre d’introduction
Page 3 sur 4
Le nombre de chiffres significatifs avec lequel un résultat est exprimé doit être en accord avec l’incertitude
absolue calculée.
Exemples : Pour une valeur  calculée à partir de grandeurs , , etc., les règles simplifiées peuvent être
appliquées :
- Si  résulte d’additions ou de soustractions, par exemple      .
- Si  résulte de multiplications ou de divisions, par exemple     
.
Application : Un objet de masse    tombe d’une hauteur    au dessus du
sol. L’intensité de pesanteur du lieu est   .
Calculer l’énergie potentielle de pesanteur Epp de l’objet à l’altitude h assortie de son incertitude.
Donnée : ∆Epp / Epp = ∆m / m + ∆g / g + ∆h / h
2. Chiffres significatifs et calculs (rappels)
Le résultat d’un calcul ne doit pas être exprimé avec une précision supérieure à celle de la donnée
utilisée la moins précise.
Conséquences :
- Après une multiplication et/ou une division, le résultat ne doit pas comporter plus de chiffres significatifs
que le nombre qui en a le moins.
Exemple : 234,45 / 42,3 x 2,3 = 12,747872 doit être arrondi à 13 car le nombre du calcul qui a la moins de
chiffres significatifs est 2,3 (il a deux chiffres significatifs), on doit donc exprimer le résultat du calcul avec 2
chiffres significatifs.  234,45 / 42,3 x 2,3 = 13.
- Après une addition et/ou une soustraction, le résultat ne doit pas comporter plus de décimales que le
nombre qui en a le moins.
Exemple : 20,312 + 9,5 +420,7 = 450,512. Le résultat doit comporter une décimale.  20,312 + 9,5 +420,7
= 450,5.
Remarque : Lorsque l'on effectue un calcul avec plusieurs étapes, les résultats des étapes intermédiaires
ne doivent pas être arrondis. Il n'y a que le résultat final qui doit comporter le bon nombre de chiffres
significatifs. Cela permet d'éviter de faire des erreurs d'arrondi qui pénaliseraient le calcul suivant.
IV. Intérêt expérimental de la notion d’incertitude
La prise en compte des incertitudes permet :

Chapitre d’introduction
Page 4 sur 4
- d’identifier les sources d’erreurs sur chaque grandeur, qu’elles soient liées à l’instrumentation de
mesure ou à son utilisation. Cela permet d’améliorer la méthode expérimentale ou d’estimer le
crédit qui peut être donné aux conclusions qui en découlent ;
- d’aider à décider si une mesure doit être conservée ou pas ;
- de commenter les résultats expérimentaux, par exemple en comparant, à l’aide de la notion
d’écart relatif, la grandeur mesurée à une grandeur de référence (attendue). La mesure est
d’autant plus satisfaisante que cet écart relatif est petit (inférieur à 5%).
EXERCICES
1. Ecrire sous la forme   les valeurs suivantes :
3,4 à 0,2 près ;
La valeur est dans l’intervalle [9,24 ; 9,30] ;
5,93 à 1% près ;
50,3 à 0,2% près.
2. Donner l’intervalle de confiance pour les valeurs suivantes :
3,9 ± 0,3 m ;
12.10-3 ± 0,005 g ;
8,15 mol.