SLCI : Transformée de Laplace, Analyse Temporelle et Harmonique

1ère année Guillaume CHAPEY –Lycée du Parc 1
Définitions
FT &
Syst. asservi
Analyse
temporelle
Analyse
harmonique
Transformée
de Laplace

1ère année Guillaume CHAPEY –Lycée du Parc 2
Définitions
FT &
Syst. asservi
Analyse
temporelle
Analyse
harmonique
Transformée
de Laplace
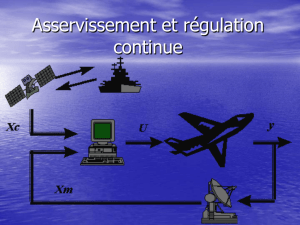
Structure d’un SLCI
Définitions
Réflexion Action
Tâche à
réaliser
Tâche
réalisée
Observation
Chaîne de retour
Chaîne d’action ou
directe
Correcteur Partie
opérative
Consigne Sortie
Capteur
+-
Comparateur
Perturbations

1ère année Guillaume CHAPEY –Lycée du Parc 3
Définitions
FT &
Syst. asservi
Analyse
temporelle
Analyse
harmonique
Transformée
de Laplace
Performances d’un SLCI
Définitions
t
s
tn%
O
1
1+
1-
n%
n%
Rapidité : caractérisée par le temps de réponse à 5%

1ère année Guillaume CHAPEY –Lycée du Parc 4
Définitions
FT &
Syst. asservi
Analyse
temporelle
Analyse
harmonique
Transformée
de Laplace
Performances d’un SLCI
Définitions
Précision : caractérisée par un écart entre l’entrée et la sortie
(ou l’entrée et une image de la sortie de même nature)

1ère année Guillaume CHAPEY –Lycée du Parc 5
Définitions
FT &
Syst. asservi
Analyse
temporelle
Analyse
harmonique
Transformée
de Laplace
Performances d’un SLCI
Définitions
Stabilité : Un système est stable si à une entrée bornée
correspond une sortie bornée