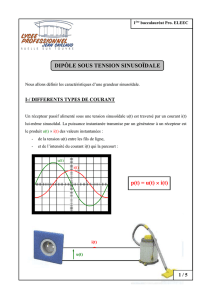
Puissance monophasée: Puissance active, réactive, apparente
Telechargé par
Ahmed Jabbour

École Nationale Polytechnique d’Alger Électrotechnique générale
CHAPITRE II
PUISSANCES EN MONOPHASÉ
La puissance électrique est une grandeur incontournable quand on veut réaliser ou dimensionner
une installation électrique. En effet, il ne suffit pas de disposer d’appareils électriques et de les
alimenter par une tension quelconque, il faut en réalité respecter les régimes pour lesquels ces
appareils ont été prévus.
Aussi, chaque machine électrique comporte une plaque signalétique fixée à un endroit bien visible
sur sa carcasse et indiquant le régime pour lequel elle a été conçue.
Ce régime est appelé « nominal »: il indique en premier lieu la tension, la fréquence, la puissance
puis le facteur de puissance, la vitesse de rotation (pour une machine tournante), le rendement
etc. La connaissance des valeurs nominales d’une machine est nécessaire pour son utilisation
correcte qui lui assure le bon fonctionnement sans défaillance, dans les limites du délai établi
(durée de vie). Par exemple, les courants et puissances ne doivent pas être dépassés sous peine
d’endommager la machine (on « grille » la machine dans ces conditions), ou alors dans certains
cas ne pas être trop en dessous de la valeur nominale sous peine de médiocrité de la performance
de la machine. En résumé, on se doit de rester, si possible, aux alentours du courant nominal
prévu pour une meilleure utilisation. Cette valeur est toujours indiquée par le constructeur.
Par ailleurs, le régime sinusoïdal qui donne lieu à des déphasages incontournables entre les
courants et tensions, met en jeu deux formes de puissances : la puissance active (liée à une
consommation purement résistive) et la puissance réactive (liée à une consommation purement
inductive ou capacitive). En séparant les deux formes de puissances, il se dégage des méthodes de
résolutions simples de toute installation électrique utilisant une source sinusoïdale.
Notons que même les choix des câbles d’alimentation d’une installation doit répondre au critère de
« courant admissible » (la section des câbles doit être choisie en fonction du courant absorbé par
l’installation). Le calcul des puissances de l’installation est alors incontournable pour pouvoir
faire ce choix.
I- Introduction
La puissance en jeu à l’intérieur d’un récepteur (ou générateur) soumis à une ddp V et
parcouru par un courant I est donnée par la relation :
PVI
Récepteur Générateur
Prenons l’exemple d’un moteur à courant continu (qui est un récepteur), alimenté sous la
tension de 200V et dont la plaque indique une puissance mécanique Pmec de 1,8kW pour
un rendement 0,9. Pour savoir quel courant nominal il va absorber, rappelons que le
rendement d’un moteur est donné par :
Chapitre2 Les puissances en monophasé Mme Dalila Sator-Namane 1

École Nationale Polytechnique d’Alger Électrotechnique générale
mec
m
elec
P
P
Et puisque le moteur est un moteur à courant continu, on peut exprimer la puissance
électrique par :
elec
PVI
Par conséquent :
mec mec mec
m
elec m
PP P 1800
I1
P VI V 200.0,9
0A
Pour un générateur à courant continu, l’expression du rendement est inversée puisque le
générateur absorbe une puissance mécanique et fournit une puissance électrique :
elec
g
mec mec
PVI
PP
Si le rendement de ce générateur est de 0,8 et si la plaque indique une puissance
électrique de 2kW, pour une tension de 200V, le générateur absorbe un courant et une
puissance mécanique de :
elec elec
mec
g
PP
2000 2000
I 10A P 2500W
V 200 0,8
II-Les Puissances en régime sinusoïdal
Contrairement au cas du régime continu, les courants et tensions sont non seulement
variables en fonction du temps mais ils présentent dans la plupart des cas des
déphasages qui conduisent à une puissance qui ne peut pas être constante dans le temps.
Aussi, il faut revenir aux expressions instantanées des tensions et courants pour
exprimer la puissance à chaque instant et dégager ainsi une puissance moyenne capable
de se transformer en une autre forme d’énergie (voir exemples plus haut pour le courant
continu).
1) Puissance instantanée
Dans le cas où un récepteur est alimenté
par une tension v(t), celui-ci consomme,
en fonction des éléments qui le
constituent, un courant j(t) : il absorbe
donc à chaque instant la puissance
instantanée définie par :
)t(j).t(v)t(p
Si la tension est sinusoïdale, l’expression
de p(t) devient :
VJ
VJ
p(t) V 2 sin( t ).J 2 sin( t )
2VJ sin( t ).sin( t )
En utilisant les formules trigonométriques, on obtient :
JV VJ
p(t) VJ cos( ) VJ cos(2 t )
Chapitre2 Les puissances en monophasé Mme Dalila Sator-Namane 2

École Nationale Polytechnique d’Alger Électrotechnique générale
On peut constater que la puissance absorbée est composée de deux termes : le premier,
indépendant du temps et toujours positif, puis le second, sinusoïdal, de fréquence
double de la fréquence du réseau. Le deuxième terme dépend du temps et change de
signe à chaque demi-période : on appelle cette quantité la puissance fluctuante parce que
justement, elle exprime une puissance absorbée puis restituée, puis absorbée etc.
2) Puissance active
En régime sinusoïdal, on définit la
puissance active comme étant la
valeur moyenne de la puissance
instantanée sur une période (figure
ci-contre).
Il s’agit donc d’une puissance qui
correspond à une fourniture réelle
d’énergie transmise au récepteur et
convertible en chaleur ou en
travail. En d’autres termes, ce qui
exprime la consommation ou non
de puissance n'est pas sa valeur
instantanée, mais sa valeur moyenne.
L'expression de la puissance moyenne ou active est donnée en toute généralité par:
T
0
T
0
dt).t(j).t(v
T
1
dt).t(p
T
1
P
Dans le cas particulier d’un régime sinusoïdal, le résultat de l’intégrale donne :
JV
P V.J.cos( ) V.J.cos [Watts]
Prenons l’exemple d’un moteur alimenté sous la tension de 400V, 50Hz et supposons
que son rendement est de 0,9 pour une puissance utile (mécanique) de 7,2kW et que le
cos est égal à 0,8. Le courant absorbé se calcule de la même façon que pour le moteur à
courant continu sauf que le facteur cos doit être pris en considération :
mec mec mec
m
m
PP P 7200
J1
P VJ cos V cos 400.0,8.0,9
2,5A
Il faut noter que la puissance active est exprimée en Watts, et ce pour la différencier
des autres types de puissances, réactives et apparentes (paragraphes suivants).
3) Puissance apparente et puissance réactive
Pour des éléments non-consommateurs comme l'inductance par exemple, la puissance
instantanée est parfois positive (l'inductance se charge en courant, donc soutire de
l'énergie au circuit), parfois négative (l'inductance restitue de l'énergie au circuit
électrique), il s’agit d’une puissance fluctuante. Pour bien comprendre ce phénomène,
représentons la valeur instantanée de la puissance pour deux cas extrêmes : la charge
purement résistive et la charge purement réactive (capacitive dans le cas présenté) :
Chapitre2 Les puissances en monophasé Mme Dalila Sator-Namane 3

École Nationale Polytechnique d’Alger Électrotechnique générale
=2
2
φ= 0 φ
v(t) = V 2sinωt j(t) = J 2sinωt v(t) = V 2sinωt j(t) = J 2sin ωt+
On note une différence fondamentale entre les deux situations.
Dans le premier cas ( ), on voit bien que la puissance moyenne sur une période est
non nulle et que la valeur de la puissance instantanée est toujours positive. Il existe
cependant une composante fluctuante qui est due à la nature périodique de la puissance
instantanée.
φ=0
Dans le deuxième cas, la valeur moyenne de la puissance est strictement nulle et il ne
peut y avoir aucune conversion possible, contrairement au cas précédent.
Pourtant, même si aucune puissance active n’est mise en jeu, un courant, bien réel, circule
dans ce type de circuits. Il s’agit donc d’associer à ces derniers une puissance dite
« réactive » et de la quantifier, tout en respectant les équations électriques découlant de
la loi d’Ohm généralisée. En effet, supposons qu’on alimente un récepteur sous la
tension V
v(t) V 2 sin( t )
et qu’un courant J
j(t ) J 2 sin( t )
en découle. Cela
signifie qu’on a en complexe :
J
Vjφ
jφ
V = Ve J = J.e
Si on multiplie le courant complexe avec le conjugué Vde la tension V, on peut établir
une expression qui illustre ce qu’on appelle la puissance apparente complexe (notée S)
absorbée par le récepteur :
V V étant le conjugué de V V
-jφ
S = J V = Ve
En développant l’expression de S, on trouve :
J
J
Puissance active Puissance réactive
V V
Vjφ-φ
-jφjφj
S = J = Ve J e = VJe = VJe = VJcos + j VJsin
On établit donc que la partie réelle de la puissance apparente complexe n’est rien d’autre
que la puissance active et on définit comme étant la puissance réactive, notée Q,
l’expression de la partie imaginaire de S:
S = P + jQ avec P = VJcos et Q = VJsin
Remarques importantes
Les puissances apparentes et réactives n’étant pas des puissances convertibles, on ne les
exprime pas avec les mêmes unités que la puissance active.
L’unité de la puissance apparente est le Volt-Ampère ou V.A.
L’unité de la puissance réactive est le V.A.R ou Volt-Ampère-Réactif.
Chapitre2 Les puissances en monophasé Mme Dalila Sator-Namane 4

École Nationale Polytechnique d’Alger Électrotechnique générale
Pour résumer on a :
VAR S= P2 Q2 VAP = VJcos W Q = VJsin
Il faut aussi souligner que même si les capacités pures ou selfs pures ne consomment
aucune énergie active, il n’en demeure pas moins qu’un courant réel les traverse et qu’il
est indispensable de quantifier leur consommation dans un circuit quelconque. C’est
justement la puissance réactive qui illustre cette consommation: une capacité qui
consomme un courant de 10A par exemple est certainement différente d’une capacité
absorbant un courant de 100A !
Pratiquement, on verra que le rôle de la puissance réactive est décisif dans les
phénomènes de conversion électromagnétique de l’énergie. Par exemple, c’est grâce à la
puissance réactive ou magnétique que l’on peut réaliser des transformateurs, des
moteurs, etc.
La puissance réactive peut également causer des désagréments comme par exemple
provoquer des chutes de tensions dans les lignes (pertes inductives) ou au contraire
causer de fortes surtensions (effet capacitif ou effet Ferranti) dans les longues lignes à
haute tension, mais ceci est une autre histoire…
Notons par ailleurs que, pratiquement, la détermination de la puissance apparente
consommée par un groupe de récepteurs permet de déduire efficacement le courant
global absorbé et conduit par conséquent à un dimensionnement pratique et rapide des
sections des câbles d’alimentation.
4) Courants actif et réactif
On définit les courants efficaces actif Ja et réactif Jr comme étant :
ar
J J cos J J sin
Le courant réel J est appelé courant apparent, puisqu’il est directement lié à la puissance
apparente. En prenant , le courant complexe s’exprime comme:
V0
ar
JJcos jJsin J jJ
5) Représentation complexe des puissances et courants
En prenant , on peut illustrer les puissances et
courants dans le plan complexe (figure ci-contre).
V0
L’axe des réels devient l’axe des puissances actives ou
axe P, et l’axe des imaginaires devient celui des
puissances réactives Q. On a alors :
a
PVJ et
r
QVJ
Si la tension n’est pas origine des phases, les
courants actif et réactif sont déterminés par les
projections de Jsur l’axe colinéaire à V(et qui
sera alors l’axe P) puis sur l’axe
perpendiculaire à l’axe P et qui sera l’axe Q
(voir figure ci-contre).
Les parties réelle et imaginaire n’ont dans ce
cas aucun sens physique, contrairement à Ja et
Jr qui représentent respectivement les
puissances active et réactive.
Chapitre2 Les puissances en monophasé Mme Dalila Sator-Namane 5
 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
 13
13
 14
14
 15
15
 16
16
 17
17
 18
18
 19
19
 20
20
 21
21
 22
22
 23
23
1
/
23
100%