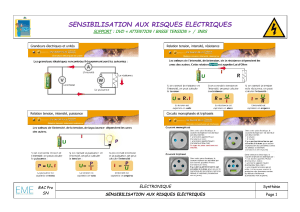
COURS MACHINES ELECTRIQUES

COURS MACHINES
ELECTRIQUES
PAR MOUHAMADOU THIAM
COURS MACHINES ELECTRIQUES 1

PLAN
COURS MACHINES ELECTRIQUES 2
CHAPITRE 1 : TRANSFORMATEURS
1.1 Symboles
1.2 Principe - Équations
1.2.1 Constitution - Principe
1.2.2 Équations
1.3 Transformateur idéal
1.3.1 Transformateur parfait
1.3.2 Impédance ramenée
1.4 Transformateur réel à vide
1.4.1 Influence de la réluctance du circuit magnétique
1.4.2 Influence des pertes
1.5 Transformateur réel en charge
1.5.1 Schéma équivalent
1.5.2 Chute de tension
1.5.3 Essais et propriétés du transformateur
1.6 Transformateurs spéciaux
1.6.1 Autotransformateur
1.6.2 Transformateur de tension (TT)
1.6.3 Transformateur de courant (TI)
1.7 Transformateur triphasé
1.7.1 Grandeurs caractéristiques d’un transformateur triphasé
1.7.2 Rapport de transformation
1.7.3 Groupes de
1.7.4 Conditions du couplage en parallèle
1.8 Mise sous tension des transformateurs
2.1 Technologie des machines électriques
2.1.1 Matériaux magnétiques
2.1.2 Matériaux conducteurs
2.1.3 Matériaux isolants - Classe d’isolation
2.2 Services de marche
2.2.1 Échauffement des machines électriques
2.2.2 Indice de protection IPxx et IKxx
2.2.3 Plaque signalétique
2.3 Lois générales de la conversion électromécanique
2.4 Production de forces électromotrices
2.4.1 Structure de la machine
2.4.2 Flux magnétique
2.4.3 Force électromotrice induite
2.5 Inductions tournantes
2.5.1 Inducteur tournant
2.5.2 Inducteur triphasé fixe
2.6 Machine bipolaire équivalente
2.7 Explication microscopique du fonctionnement
CHAPITRE 2 : GENERALITES SUR LES MACHINES
ELECTRIQUES TOURNANTES

COURS MACHINES ELECTRIQUES 3
3.1 Symboles
3.2 Constitution d’une machine à courant continu
3.2.1 L’inducteur
3.2.2 L’induit
3.2.3 Collecteurs et balais
3.3 Équation générale
3.3.1 Force électromotrice à vide
3.3.2 Étude en charge
3.4 Moteur à courant
3.4.1 Démarrage d’un moteur
3.4.2 Moteur à excitation séparée (ou dérivée)
3.4.3 Moteur à excitation série
3.4.4 Moteur à excitation composée
3.4.5 Rendement d’un moteur - couple utile
3.4.6 Mise en œuvre des moteurs
3.5 Génératrices à courant continu
3.5.1 Freinage rhéostatique
3.5.2 Génératrice tachymètrique
3.5.3 Annexe : génératrices auto-excitées
CHAPITRE 3 : MACHINES A COURANT CONTINU
4.3.2 Diagramme de Blondel
4.4 Couplage des alternateurs
4.4.1 Condition préalable au couplage
4.4.2 Répartition des puissances entre deux alternateurs
4.4.3 Conséquences des fautes de couplage
4.4.4 Répartition optimale des puissances
CHAPITRE 4 : MACHINES SYNCHRONES
4.1 Symboles
4.2 Construction - Principe
4.2.1 Force électromotrice
4.2.2 Fonctionnement en charge
4.3 Alternateur autonome
4.3.1 Machine synchrone couplée au réseau
5.1 Symboles
5.2 Structure - Principes de fonctionnement .
5.2.1 Structure
5.2.2 Principes de fonctionnement
5.2.3 Glissement - fréquences rotoriques
5.3 Équations - Schéma équivalent
5.3.1 Équations
5.4 Étude du courant et du couple
5.4.1 Courant absorbé -Diagramme du cercle
5.4.2 Échelle de glissement - Puissances
5.4.3 Étude directe du couple
5.5 Mise en œuvre de la machine. asynchrone
5.5.1 Caractéristiques du moteur asynchrone
5.5.2 Démarrage du moteur asynchrone
5.5.3 Réglage de la vitesse
5.5.4 Réversibilité - Freinage
5.6 Moteur asynchrone monophasé
CHAPITRE 5 : MACHINES ASYNCHRONES

COURS MACHINES ELECTRIQUES 4
CHAPITRE 1 : TRANSFORMATEURS
Le transformateur est un convertisseur « alternatif-alternatif » qui permet de modifier la valeur
efficace d’une tension alternative en maintenant la fréquence et la forme de l’onde inchangées.
Les transformateurs sont réalisés en toutes puissances et tensions, de quelques VA et à basse
tension pour l’alimentation de circuits électroniques à quelques centaines de MVA et de kV
pour l’alimentation ou le couplage des réseaux de transport de l’énergie électrique.
Le transformateur est également utilisé comme adaptateur d’impédance en électronique.
Nous étudierons tout d’abord le transformateur monophasé et nous verrons comment en déduire
les propriétés des transformateurs triphasés.

COURS MACHINES ELECTRIQUES 5
1.1 Symboles
On peut employer deux symboles pour représenter le transformateur monophasé. Sur
celui de la Figure 1.1 (a), les trois barres verticales symbolisent le noyau magnétique qui
permet à l’énergie magnétique de passer du bobinage primaire au bobinage secondaire.
(a) Symbole du transformateur monophasé. (b) Symbole du transformateur monophasé.
FIGURE 1.1 –Symboles du transformateur.