Rappel
P
Ni
URI
=
−E
iP
N
Ri
E
i
Rappel
Loi de Kirchhoff
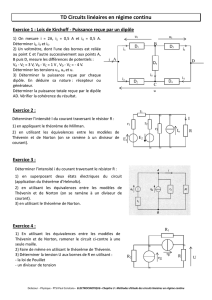
Déterminer le courant I
Cherchons la valeur des courants I1, I2et I3dans le circuit
Loi de Kirchhoff
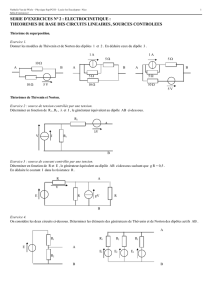
Appliquer les lois de Kirchhoff au circuit suivant afin de déterminer les
valeurs et les sens corrects des courants I1, I2et I3. Préciser ensuite la
fonction des trois accumulateurs et, enfin, calculer le potentiel du
point B si l’on relie le point A à la masse (VA= 0).
Les sens des courants sont
choisis arbitrairement. on
constate que seul le
sens du courant I3 doit être
modifié. Les trois
accumulateurs sont des
générateurs
Loi de Kirchhoff
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
1
/
35
100%
