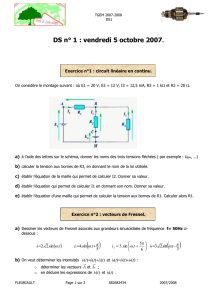
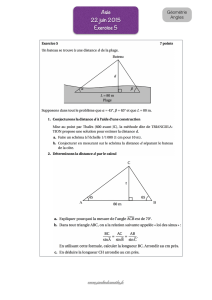
Exercices (Séries de Fourier et Espaces de Hilbert)

Université Lille 1 — Licence de Mathématiques (L3, 2006/07)
MATH 312 — Responsable: J.-F. Burnol
Exercices en surplus :
XCVIII Les gramiens définis dans les exercices précédents pour des vecteurs dans un espace
hermitien existent aussi avec les mêmes formules pour des vecteurs dans un espace euclidien, en
particulier dans RN muni de sa structure euclidienne canonique. Soient v1 , . . ., vN , des vecteurs
dans RN . Montrer que le volume du parallélotope t1 v1 + · · · + tN vN , 0 ≤ t1 ≤ 1, . . ., 0 ≤ tN ≤ 1
est la racine carrée du gramien des vecteurs v1 , . . ., vN . Le volume est calculé par rapport à la
mesure de Lebesgue canonique, qui donne masse 1 à l’hypercube unité.
XCIX (Inégalité de Hadamard) Montrer g(v1 , . . . , vn ) ≤ (v1 , v1 ) . . . (vn , vn ) avec égalité
si et seulement si soit les vecteurs vj sont mutuellement perpendiculaires soit l’un d’entre eux
est le vecteur nul. Soit A = (aij )1≤i,j≤n une matrice carrée complexe ou réelle quelconque.
Interpréter A∗ A comme une matrice de Gram 23 et en déduire l’inégalité de Hadamard :
Y s X
|aij |2
| det(A)| ≤
1≤j≤n
1≤i≤n
C (séparabilité) On se donne un espace de Hilbert V . Si V est de dimension finie alors il
a une base orthonormée (finie). On suppose V de dimension infinie. On suppose que l’on peut
trouver des vecteurs u0 , u1 , . . .qui ont la propriété que la suite (un )n=0,1,... est partout dense
dans V : tout vecteur est limite d’une suite extraite. Montrer que le seul vecteur perpendiculaire
à tous les un est le vecteur nul. On pose H0 = {0} et l’on note Hn l’espace vectoriel engendré
par u0 , . . ., un−1 . Montrer qu’il y a une infinité de n ≥ 1 tel que dim Hn = 1 + dim Hn−1 .
On les note 1 ≤ n1 < n2 < . . . . Enfin on choisit ek de norme 1 dans Hnk perpendiculaire à
Hnk −1 . Montrer que chaque un est combinaison linéaire finie des ek , k ≥ 1. En déduire que les
ek , k ≥ 1 forment un système complet, et aussi orthonormé, dans V . En déduire que (ek ) est
une base orthonormée dénombrable de V . Réciproquement si V possède une base orthonormée
dénombrable montrer que l’on peut former une suite de vecteurs partout dense. On dit que
l’espace de Hilbert est séparable. La séparabilité est donc la condition nécessaire est suffisante
pour l’existence d’une base orthonormée dénombrable 24 . En utilisant la notion de séparabilité,
prouver que si V possède une base orthonormée dénombrable alors tout sous espace fermé de
V possède aussi une base orthonormée dénombrable.
CI (deuxième formule de la moyenne) La deuxième formule de la moyenne est aux
fonctions ce que la sommation d’Abel-Dirichlet (exercice L) est aux séries. Soit φ décroissante
positive sur [x, y], soit f intégrable sur cet intervalle, alors :
Z t
Z y
(φ décroissante positive)
φ(t)f (t)dt ≤ φ(x) sup f (u)du
x≤t≤y
x
x
Remarquez bien que les valeurs absolues sont à l’extérieur des intégrales. Faites la preuve :
1. pour φ de classe C 1 et f continue, par une intégration par parties,
23. prendre comme vecteurs les conjugués complexes des colonnes de A
24. finie ou infinie : notre convention est que les ensembles finis sont dénombrables.
21
2. en toute généralité en admettant qu’après avoir modifié φ(t) en au plus unRnombre dénombrable de points pour qu’elle soit continue à droite 25 on peut écrire φ(t) = ]t,y] dµ(u)+φ(y)
avec µ une mesure positive et en utilisant Fubini.
Pour encore une autre méthode de preuve, voir le texte Théorème de Dirichlet sur le site de
votre Professeur. Lorsque f est à valeurs réelles justifier alors :
∃ξ ∈]x, y[
Z
y
+
φ(t)f (t)dt = φ(x )
x
Z
ξ
−
f (t)dt + φ(y )
x
Z
y
f (t)dt
ξ
valable pour toute φ monotone (pas seulement décroissante positive).
−1 qui est moCII En appliquant la deuxième formule de la moyenne à la fonction
sin(x/2)
R π
dt ≤ π(N + 11) sin( a ) ,
notone sur l’intervalle d’extrémités a et π (0 < a < 2π), prouver a DN (t) 2π
2
2
R
b
1
1
dt 1
et en déduire pour 0 < a < b < 2π : a DN (t) 2π ≤ (N + 1 )π sin( a ) + sin( b ) . Montrer plus
2
2
2
généralement |(DN ∗ 1]a,b[ )(x)| ≤ (N +1 1 )π sin( 1a−x ) + sin( 1b−x ) pour b − 2π < x < a. En déduire
2
2
2
que si φ est une fonction en escalier, identiquement nulle sur ]u, v[ (avec u < 0 < v) alors la série
de Fourier Dn ∗ φ converge uniformément vers zéro sur tout sous-intervalle [u′ , v ′ ] ⊂]u, v[ fermé.
En déduire que si f et g sont deux fonctions intégrables qui coïncident sur ]u, v[ la différence
SN (f ) − SN (g) converge uniformément vers 0 sur tout sous-intervalle [u′ , v ′ ] ⊂]u, v[ fermé.
P
CIII On revient au problème de borner uniformément les sn (x) = 1≤k≤n sin(kx)
. On peut
k
1
supposer 0 < x ≤ π (pourquoi ?). On pose uk (x) = sin(kx), vk = k , pour k ≥ 1 (et u0 (x) = 0).
On note An (x) = u1 (x)+· · ·+un (x). Montrer |An (x)| ≤ sin(x/2)−1 et même |An(x)−Am (x)| ≤
P
sin(kx) 1
1
sin(x/2)−1 pour tout n, m. En déduire (par sommation d’Abel) ∞
≤ sin(x/2)
k=n+1
k
n+1 .
Montrer alors :
nx ≥ π =⇒ |sn (x)| ≤
x
π
2
π−x
+
< +
2
π sin(x/2)
2 π
(= 2.2074 . . . )
Pour 0 < nx < π prouver en utilisant une somme de Riemann (on observera que la fonction sin(x)
x
Rπ
dt
(=
1.8519
.
.
.
).
En
déduire
est strictement décroissante sur ]0, π]) : 0 < sn (x) < 0 sin(t)
t
X
sin(kx) π
2
∀x ∈ R ∀n ≥ 1
< 2 +π
k
1≤k≤n
Rπ
En fait, c’est bien 0
de votre Professeur.
sin(t)
t dt
qui est la borne optimale. Se reporter à l’annexe Gibbs sur le site
CIV (un théorème de Cantor) Il semble que Riemann connaissait le résultat suivant mais qu’il n’en ait pas donné explicitement la preuve : si pour tout x il est vrai que
limn→∞ (an cos(nx) + bn sin(nx) = 0) alors lim an = 0 et lim bn = 0. Ce n’est pas un résultat
évident, lorsque vous y aurez suffisamment réfléchi reportez vous au texte Cantor-Lebesgue sur
le site de votre Professeur.
25. autrement dit on remplace φ(t) par φ(t+ ).
22