Corrigé DS N°02 - MPSI Saint

CORRIGÉ DU DEVOIR SURVEILLÉ N˚02
PROBLÈME 1
Partie I. Etude de Arcsin (sin 2x)
On considère la fonction ϕ : R → R définie pour tout x ∈ R par
ϕ(x) = Arcsin (sin 2x).
1.
La fonction ϕ est définie sur R. De plus, les fonctions sin et Arcsin étant
impaires, ϕ est impaire. Enfin, comme sin est 2π-périodique, x 7→ sin(2x)
est π-périodique. Il en va de même de ϕ. On pourra mener l’étude sur [0, π2 ]
puis compléter par symétrie centrale. Enfin, comme ϕ( π2 − x) = ϕ(x), la
droite d’équation x = π4 est axe de symétrie.
Résumons, ϕ est impaire et π-périodique.
N
2.
• Soit x ∈ [0, π/4]. En ce cas, 2x ∈ [0, π/2]. Par conséquent, 2x est
l’unique antécédent de sin(2x) appartenant à [−π/2, π/2], c’est-à-dire
ϕ(x) = Arcsin sin(2x) = 2x
• Soit x ∈ [π/4, π/2]. En ce cas, 2x ∈ [π/2, π]. D’où π − 2x ∈ [0, π/2].
Comme de plus,
sin(2x) = sin(π − 2x),
π − 2x est l’unique antécédent de sin(2x) appartenant à [−π/2, π/2],
c’est-à-dire
ϕ(x) = Arcsin sin(2x) = π − 2x
N
3.
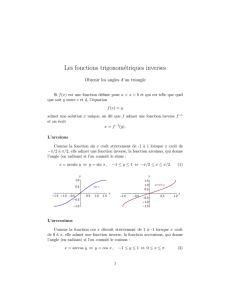
D’après les propriétés de symétrie de ϕ, il suffit de la représenter sur [0, π/4],
de compléter par symétrie par rapport à la droite x = π4 , puis par symétrie
centrale et enfin de translater le graphe ainsi obtenu. On obtient ainsi
N
Partie II. Étude de Arcsin
1.
2x
1 + x2
2x
.
Soit f la fonction définie par f (x) = Arcsin
1 + x2
Intervalle d’étude
a. Soit x ∈ R, on déduit de l’inégalité (1 − |x|)2 ≥ 0 que 2|x| ≤ 1 + x2 . De
plus, il y a égalité précisément lorsque |x| = 1.
N
1
b. La fonction Arcsin
sur [−1, 1]. Or, d’après la question précédente,
est définie
2x
appartient à [−1, 1]. Par composition, f est donc
pour tout x ∈ R,
1 + x2
définie sur R.
N
−2x
2x
c. Soit x ∈ R, f (−x) = Arcsin
= −Arcsin
= −f (x).
1 + x2
1 + x2
Par suite f est impaire.
N
2. Tableau de variation
a. Soit t ∈] − π/2, π/2[, nous avons sin t
2 cos
2 tan t
2 sin t cos t
t
= sin(2t)
2t =
2 =
sin
1 + tan t
cos2 t + sin2 t
1 + cos2 t
2 tan t
Ainsi, f (tan t) = Arcsin
= Arcsin (sin 2t) = ϕ(t).
N
1 + tan2 t
b. Soit x ∈ R, Posons t = Arctan (x), de sorte que t ∈] − π/2, π/2[ et x =
tan t. D’après la question précédente, il s’ensuit immédiatement que f (x) =
ϕ(t) = ϕ ◦ Arctan (x).
N
c. D’après les résultats de la Partie I
◮ ϕ est strictement décroissante sur ] − π/2, −π/4],
◮ ϕ est strictement croissante sur ] − π/4, π/4[,
◮ ϕ est strictement décroissante sur [π/4, π/2[.
La fonction Arctan : R →] − π/2, π/2[ est une bijection strictement croissante est continue. D’après le Théorème de la bijection, elle réalise des
bijections strictement croissantes de
⊲ de ] − ∞, −1] sur ] − π/2, −π/4],
⊲ de ] − 1, 1[ sur ] − π/4, π/4[,
⊲ de [1, ∞[ sur [π/4, π/2[,
Par composition de deux fonctions monotones, nous en déduisons que
f est strictement décroissante sur ] − ∞, −1],
f est strictement croissante sur ] − 1, 1[,
f est strictement décroissante sur [1, ∞[.
N
d. Le tableau suivant résume les variations f :
x
−∞
f (x)
−1
0
0
0
ց
− π2
1
ր
π
2
+∞
ց
0
ր
Pour le calcul des limites en ±∞, procédons par composition : effectuons le
changement de variable y(x) = Arctan x, il vient :
π
2
ϕ(y) −−−−−→ 0
• y(x) = Arctan (x) −−−−→ ±
x→±∞
•
Par composition des limites, il s’ensuit que
y→±π/2
lim f (x) = 0.
x→±π/2
2
N
on
utiliser
peut
les
aussi
formules
de la paramétrisation
rationnelle du cercle
privé d’un point
3.
Représentation graphique
2x
∈] − 1, 1[, pour tout x différent de 1 et −1.
a. D’après la question 1.a,
1 + x2
Comme Arcsin est dérivable sur ] − 1, 1[, il en résulte par composition que
f est dérivable sur R \ {±1}. De plus, pour tout x différent de 1 et −1., on
a:
1
′
f (x) = q
1−
=
Ainsi,
◮
◮
4x2
(1+x2 )2
1
2(1 + x2 ) − 4x2
2(1 − x2 )
=p
×
×
(1 + x2 )2
1 + x2
(1 + x2 )2 − 4x2
2
2
1 − x2
p
=±
×
2
1+x
1 + x2
(1 − x2 )2
2
.
1 + x2
2
Pour tout x ∈] − ∞, −1[∪]1, +∞[, 1 − x2 < 0 et f ′ (x) = −
.
1 + x2
Pour tout x ∈] − 1, 1[, 1 − x2 > 0 et par conséquent f ′ (x) =
N
b. Étude de quelques tangentes
Rappelons que si f est dérivable au point a, son graphe admet une tangente
au point d’abscisse a, elle a pour équation
y = f (a) + f ′ (a)(x − a)
Au point d’abscisse 0, on a f (0) = 0 et f ′ (0) = 2. Par suite, la tangente
T0 a pour équation
y = 2x.
√ √
1
2/ 3
√
√
=
Au point d’abscisse
∈] − 1, 1[, on a f (1/ 3) = Arcsin 1+1/
3
3
√
√
π
3
2
Arcsin ( 3/2) = et f ′ (1/ 3) = 4/3
= . Par suite la tangente T1/√3
3
2
a pour équation
1
π 3
y = + (x − √ ).
3 2
3
√
√
√
π
Au point d’abscisse 3 ∈]1, +∞[, on a f ( 3) = et f ′ ( 3) = − 24 =
3
1
− , de sorte que la tangente T√3 a pour équation
2
y=
√
π 1
− (x − 3)
3 2
N
c.
Soit 0 < x < 1. D’après la question 3a. f ′ (x) =
par OPA que lim− f ′ (x) = 1.
2
. Il en résulte
1 + x2
x→1
Soit x > 1. D’après la question 3a. f ′ (x) = −
OPA que lim+ f ′ (x) = −1.
x→1
3
2
. Il en résulte par
1 + x2
d.
Ainsi, ℓ+ = −1 et ℓ− = 1.
N
EXERCICE 1
1.
Soit x une solution de (1). En ce cas, 2x ∈ [−1, 1], soit |x| ≤ 12 . et
√ x = sin(Arcsin (x)) = sin Arcsin (2x) − Arcsin (x 3)
√ √
= 2x cos Arcsin (x 3) − x 3 cos (Arcsin (2x))
√ √
√
= 2x 1 − 3x3 − x 3 1 − 4x2
N
2.
Soit x ∈
[− 21 , 12 ].
√
√ √
x = 0 ou 2 1 − 3x2 − 3 1 − 4x2 = 1
√
x = 0 ou 1 − 4x2 = 0
1
1
⇐⇒ x = 0 ou x = − ou x =
2
2
1 1
Autrement dit, si x est solution de (1), alors x ∈ {0, − , }.
2 2
Inversement, on vérifie que ces trois valeurs sont effectivement solutions de
(1).
N
x est sol de (2)
⇐⇒
⇐⇒
EXERCICE 2
1.
Posons A = Arctan xy + Arctan
deux étapes :
y−x
. Pour déterminer A on procède en
y+x
Attention au signe
1 Calcul de tan(A)
y−x
x
tan
Arctan
+
tan
Arctan
y
y+x
x
y−x
tan Arctan + Arctan
=
y−x
x
y
y+x
1 − tan Arctan y tan Arctan y+x
=
x
y
y−x
y+x
x y−x
y y+x
+
1−
4
=
x2 + y 2
= 1.
x2 + y 2
dans la formule d’addition pour les tangentes
tan(a+b) =
tan a + tan b
1 − tan a tan b
2 Localisation de A : Par ailleurs, comme 0 <
croissance de la fonction Arctan on a Arctan 0 <
π
d’où :
4
Arctan
x
y
< 1 et 0 < y−x
< 1 par
y+x
y−x
π
< 4 et 0 < Arctan y+x
<
x
y
y − x i πh
x
.
+ Arctan
∈ 0,
y
y+x
2
3 Conclusion : comme A a pour tangente 1, on en déduit
Arctan
2.
x
y−x
π
+ Arctan
= .
y
y+x
4
Tout d’abord, comme 15 ∈]0, 1[, Arctan 51 ∈]0, π4 [, donc 4Arctan 51 appartient
à l’intervalle ]0, π[. Par ailleurs, on a
2
2 tan Arctan 15
1
5
5
tan 2Arctan
=
=
,
1 =
1
2
5
12
1 − 25
1 − tan Arctan 5
puis : tan 2a =
2 tan a
1−tan2 a
10
2 tan 2Arctan 15
1
120
12
tan 4Arctan
=
.
=
25 =
1
2
5
119
1 − 144
1 − tan 2Arctan 5
Comme tan 4Arctan 51 > 0 et 4Arctan 15 ∈]0, π[, 4Arctan 51 ∈]0, π2 [ ; on
120
déduit alors de l’égalité précédente que 4Arctan 51 = Arctan 119
.
3.
On applique la question 1 à x = 1 et y = 239 :
Arctan
=
Comme Arctan 119
120
ment :
π
2
119
π
1
+ Arctan
= .
239
120
4
− Arctan 120
=
119
π
2
− 4Arctan 51 , on obtient finale-
1
1
π
= 4Arctan − Arctan
.
4
5
239
de π en 1706.
EXERCICE 3
1.
La fonction ch est définie sur R et ne s’y annule pas. Par conséquent, son
inverse (la fonction sch) est définie sur D = R. Comme la fonction ch est
paire, la fonction sch est également paire.
N
2.
Tout d’abord, la limite de sch en −∞ et en +∞ est 0 puisque la limite de
ch est +∞ en ±∞. Par ailleurs, la fonction sch est dérivable sur R (ch est
dérivable sur R et ne s’y annule pas) et :
ch′ (x)
sh x
=− 2 .
2
ch x
ch x
La fonction sh étant strictement positive sur R∗+ , sch’ est strictement négative
sur R∗+ . Par conséquent, sch est strictement décroissante sur R∗+ et strictement croissante sur R∗− par parité.
N
5
Cette formule per-
calculer cent décimales
N
∀x ∈ R, sch′ (x) = −
mit à John Machin de
3.
La fonction sch est continue et strictement décroissante sur [0, +∞[, d’après
le théorème de la bijection, elle réalise une bijection de [0, ∞[ vers sch([0, +∞[) =
]0, 1]. Cela montre que la restriction de sch à [0, +∞[ admet une application
réciproque.
N
4.
D’après la question précédente, l’ensemble de définition de Argsch est ]0, 1].
La fonction sch étant continue et strictement décroissante sur [0, +∞[,
Argsch est également continue et strictement décroissante sur ]0, 1]. toujours d’après le
théorème de la bijec-
y=x
tion
y = argsch x
1
y = sch x
O
1
N
5.
Soit x ∈]0, 1] et t ∈ R+ . Alors
t = Argsch(x)
1
ch (t)
⇐⇒
x = sch(t) ⇐⇒ x =
⇐⇒
1
= ch (t) ⇐⇒ t = Argch (1/x)
x
Finalement
Argsch(x) = Argch (1/x) = ln
1+
√
1 − x2
x
.
N
EXERCICE 4
1.
2.
Comme sh est une bijection de R dans R, l’équation sh x = − 12 admet une
unique solution sur R. En notant a cette solution, on a donc 2sh a + 1 = 0.
étudier
Posons u(x) = ch 2 x + sh x. La fonction u est définie, dérivable sur R et :
x 7→ 2sh x + 1.
∀x ∈ R, u′ (x) = 2ch x sh x + ch x = ch x(2sh x + 1).
Le signe de u′ est celui de 2sh x + 1 (ch est positive sur R). Comme sh
est croissante sur R, 2sh x + 1 est négatif sur ] − ∞, a] et positif sur [a, +∞[.
Cela montre que u est décroissante sur ] − ∞, a] et croissante sur [a, +∞[.
Or, comme sh a = − 12 et ch 2 a − sh 2 a = 1, on a :
u(a) = ch 2 a + sh a = 1 + sh 2 a + sh a = 1 +
1 1
3
− = ;
4 2
4
ce qui montre que u(a) est positif, donc que la fonction u est positive sur
R.
6
On
peut
la
aussi
fonction
2sh x+1 ≥ 0 ⇔ x ≥
a
3.
La fonction g est deux fois dérivable sur R et, pour x ∈ R,
g ′(x) = ch xesh x − 1
4.
g ′′(x) = (ch 2 x + sh x)esh x = u(x)esh x .
et
D’après la question précédente, g ′′ est positive, donc g ′ est croissante sur R.
Comme g ′ (0) = 0, g ′ est négative sur R− et positive sur R+ . On en déduit
que g est décroissante sur R− et croissante sur R+ (avec g(0) = 0).
On déduit de la question précédente que, pour tout x ∈ R, g(x) ≥ 0, c’està-dire :
∀x ∈ R, 1 + x ≤ esh x .
(3)
On a donc :
1
.
esh x
∀x ∈]0, 1[, esh x ≤
Il
s’agit
de
l’inégalité précédente,
∀x ∈ R, 1 − x ≤ esh (−x) ,
soit 1 − x ≤ e−sh x ou encore 1 − x ≤
appliquée à −x.
On en déduit que : 1
.
1−x
(4)
sh est impaire.
1−x >0
Les inégalités (3) et (4) démontrent l’encadrement souhaité.
5.
D’après la question précédente, on a :
∀x ∈]0, 1[,
ln(1 + x) ≤ sh x ≤ − ln(1 − x).
On en déduit que pour tout k ∈ [[n, np]],
1
1
1
≤ sh
≤ − ln 1 −
.
ln 1 +
k
k
k
En sommant ces inégalités de n à np, il vient :
X
np
np
np
X
X
k+1
1
k−1
ln
sh
ln
≤
≤−
,
k
k
k
k=n
k=n
k=n
ce qui s’écrit aussi
np
X
k=n
np
X
[ln(k − 1) − ln k] .
[ln(k + 1) − ln k] ≤ Sn ≤ −
k=n
Ainsi, on obtient : ln
6.
np + 1
n
≤ Sn ≤ − ln
n−1
np
télescopiques !
lim ln
n→+∞
np + 1
n
1
= lim ln p +
n→+∞
n
l’aide
= ln p
lim − ln
n→+∞
n−1
np
= lim − ln
n→+∞
1
1
−
p np
n→+∞
7
du
conclut
à
théorème
par encadrement.
1
= − ln
= ln p ,
p
le théorème d’encadrement montre que lim Sn = ln p.
On
d’existence de limite
et d’autre part
sommes
.
Comme d’une part Deux
N