x - maths peyramale

TS DEVOIR MAISON no3correction
Exercice 1
Soit fla fonction définie sur Rpar f(x) = x
x2+ 1 et la fonction gdéfinie sur Rpar g(x) = x3 x2+ 1 .
1. I1=Z1
0
f(x) dx.
fest de la forme 1
2
u′
uavec u(x) = x2+ 1
Une primitive de fest F(x) = 1
2ln(x2+ 1)
Donc I1="1
2ln(x2+ 1)#1
0
=1
2ln2 −1 2ln1 = 1 2ln2
2. I1+ I2=Z1
0
x
x2+ 1 dx+Z1
0
x3
x2+ 1 dx=Z1
0
x+x3
x2+ 1 dx=Z1
0
x(x2+ 1)
x2+ 1 dx=Z1
0
xdx="1
2x2#1
0
=1
2
Donc I2=1
2−I1=1 2−1 2ln2
Exercice 2
1. Zln2
0
e−x
e−x+4 dx
Soit f(x) = e−x
e−x+4
fest de la forme −u′
uavec u(x) = e−x+4
Une primitive de fest F(x) = −ln(e−x+4)
Donc Zln2
0
e−x
e−x+4 dx= [−ln(e−x+4)]ln2
0= (−ln(e−ln2 +4) −(−ln(e0+4)) = (−ln(−1/2 + 4)) + ln5 = −ln(7/2) + ln5
2. Z2
−1
t(t2+ 3)4dt
Soit f(t) = t(t2+ 3)4
fest de la forme 1
2u′u4avec u(t) = t2+ 3
Une primitive de fest F(t) = 1
2×1 5(t2+ 3)5=1 10(t2+ 3)5
Donc Z2
−1
t(t2+ 3)4dt="1
10(t2+ 3)5#2
−1
= 1
1016807!− 1 101024!= 1578,3
3. Z2e
e
1
xlnxdx
Soit f(x) = 1
xlnx
fest de la forme u′
uavec u(x) = lnx
Une primitive de fest F(x) = ln(lnx)
Donc Z2e
e
1
xlnxdx= [ln(lnx)]2e
e= (ln(ln(2e)) −(ln(ln(e)) = ln(ln2 + 1) −ln(1) = ln(ln 2 + 1)

Exercice 3
On considère la fonction fdéfinie ]0 ; +∞[ par : f(x) = xln x−1.
Partie A : Étude d’une fonction
1. a. lim
x→+∞x= +∞et lim x→+∞lnx= +∞donc lim x→+∞f(x) = +∞.
b. On sait que lim
x→0xlnx= 0, donc lim x→0f(x) = −1.
2. f′(x) = ln x+x×1
x= lnx+ 1.
f′(x)>0
lnx+ 1 >0
lnx > −1
x > e−1
On a fe−1= e−1lne−1−1 = −e−1−1.
On a donc le tableau de variations de la fonction fsur ]0 ; +∞[ suivant :
x0 e−1+∞
f′(x)−0+
f(x)
−1
−e−1−1
+∞
3. Sur i0 ; e−1h, f (x)6−1<0 donc l’équation n’a pas de solution sur cet intervalle.
Sur l’intervalle he−1; +∞h, la fonction fest continue et croissante . De plus 0 ∈h−e−1−1 ; +∞hdonc il existe un réel
unique αde l’intervalle he−1; +∞htel que f(α) = 0.
La calculatrice donne successivement : 1,76 <α<1,77.
4. – sur ]0 ; α[, f (x)<0 ;
– sur ]α; +∞[, f (x)>0.
5. f(α) = 0 soit αlnα−1 = 0 soit αln α= 1 soit lnα=1
α.
Partie B : Calcul d’une intégrale
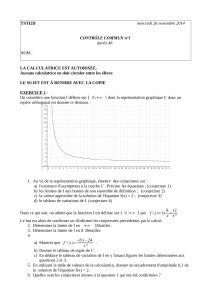
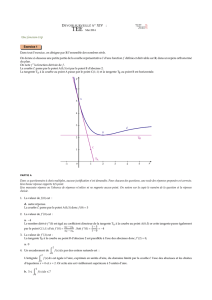
On donne en annexe la courbe C, représentation graphique de la fonction fdans un repère orthonormé. On considère
l’intégrale suivante : I = Z4
α
f(x) dx.
1. On sait que sur l’intervalle [α; 4] la fonction fest positive, donc l’intégrale est (en unité d’aire) l’aire de la surface
hachurée limitée par la courbe C, l’axe des abscisses et les droites d’équations respectives x=αet x= 4.
2. F(x) = 1
4x2(2ln x−1)
F′(x) = 1
4×2x(2ln x−1) + 1 4x2(2 x) = xlnx−1 2x+1 2x=xlnx
Ce qui prouve que F est une primitive de la fonction x7→ xlnx.
3. J = Z4
α
xlnxdx="1
4x2(2ln x−1)#4
α
= 1
416(2ln 4 −1)!− 1 4α2(2ln α−1)!= 8ln4 −4−1 2α2lnα+1 4α2

4. I = Z4
α
xlnx−1 dx=Z4
α
xlnxdx−Z4
α
1 dx= J −[x]4
α= J −(4 −α) = 8ln4 −4−1
2α2lnα+1 4α2−4 + α
= 8ln4 −8−1
2α2lnα+1 4α2+α
Or d’après la partie A question 5, ln α=1
α
donc I = 8ln(22)−8−1
2α2×1 α+1 4α2+α= 16ln2 −8−1 2α+1 4α2+α= 16ln2 −8 + 1 4α2+1 2α
I≈4,8 (u. a.) à 0,1 près.
1
2
3
4
5
−1
−2
123456
−1−2x
y
O
C